Алгоритм Укконена

Эта статья находится в разработке!

Алгоритм Укконена — алгоритм построения суффиксного дерева для заданной строки [math]s[/math] за линейное время.

Первая версия алгоритма

Рассмотрим сначала метод, который строит дерево за время [math]O(n^3)[/math], где [math]n[/math] — длина исходной строки [math]s[/math]. В дальнейшем данный алгоритм будет оптимизирован таким образом, что будет достигнута линейная скорость работы.

Описание

Алгоритм делится на [math]n[/math] фаз. В фазе с номером [math]j[/math] в дерево добавляются все суффиксы подстроки [math]s_{1..j}[/math]. При добавлении суффикса [math]s_{i..j}[/math] алгоритм сначала находит конец пути из корня, помеченного подстрокой [math]s_{i..j-1}[/math], затем добавляет к найденной вершине новое ребро с листом [math]s_j[/math], если этот символ не был добавлен ранее.

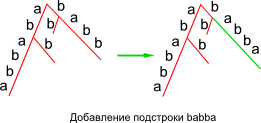
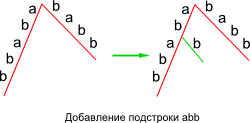
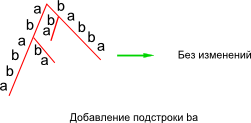
Возможные исходы операции insert

Ниже приведены три возможных случая, которые могут возникнуть при добавлении подстроки [math]s_{i..j}[/math] в дерево.

Случай	Правило	Пример
1. Продление листа	Пусть подстрока [math]s_{i..j-1}[/math] кончается в листе. Добавим элемент [math]s_j[/math] в конец последнего ребра.
2. Создание листа	Пусть подстрока [math]s_{i..j-1}[/math] кончается в вершине, не являющейся листом, из которой нет пути по символу [math]s_j[/math]. Создадим новую дугу с началом в элементе [math]s_{j-1}[/math] и листом [math]s_j[/math].
3. Ничего не делать	Пусть подстрока [math]s_{i..j-1}[/math] кончается в вершине, из которой есть путь по [math]s_j[/math]. Тогда ничего делать не надо.

Оптимизация алгоритма Укконена

Рассмотрим две леммы, позволяющие ускорить алгоритм Укконена до [math]O(n^2)[/math].

Лемма 1. Стал листом — листом и останешься

Лемма:

Если в какой-то момент работы алгоритма Укконена будет создан лист с меткой [math]i[/math] (для суффикса, начинающегося в позиции [math]i[/math] строки [math]S[/math]), он останется листом во всех последовательных деревьях, созданных алгоритмом.

Доказательство:

[math]\triangleright[/math]

Это верно потому, что у алгоритма нет механизма продолжения листового ребра дальше текущего листа. Если есть лист с суффиксом [math]i[/math], правило продолжения 1 будет применяться для продолжения [math]i[/math] на всех последующих фазах.

[math]\triangleleft[/math]

Лемма 2. Правило 3 заканчивает дело

Лемма:

В любой фазе, если правило продолжения 3 применяется в продолжении [math]i[/math], оно будет реализовываться во всех дальнейших продолжениях(от [math]i + 1[/math] по [math]j + 1[/math]) до конца фазы.

Доказательство:

[math]\triangleright[/math]

При использовании правила продолжения 3 путь, помеченный [math]S[i..j][/math] в текущем дереве, должен продолжаться символом [math]j+1[/math]⁠, и точно так же продолжается путь, помеченный [math]S[i + 1..j][/math]⁠⁠⁠⁠⁠⁠⁠⁠⁠⁠, поэтому правило 3 применяется в продолжениях [math]i + 1, i + 2, ..., j + 1[/math]

[math]\triangleleft[/math]

Когда используется правило 3, никакой работы делать не нужно, так как требуемый суффикс уже в дереве есть. Поэтому можно заканчивать каждую фазу [math]j + 1[/math] после первого же использования правила прохождения 3. Если это случится в продолжении i, то уже не требуется явно находить концы строк [math]S[k..j][/math] с [math]k \gt i[/math].

Алгоритм Укконена за квадратичное время

Рассмотрим правила продолжения суффиксов.

При использовании правила 1 по лемме 1 в последующих фазах будет выполняться правило 1. Поэтому скажем, что мы создаём лист не только для рассмотренной части строки, а для всей всей строки до конца.
При использовании правила 2 появится новый лист, который далее будет продлеваться по правилу 1.
При использовании правила 3 по лемме 2 никакой работы делать не нужно, поскольку суффикс в дереве уже есть. Следовательно, можно остановиться и не добавлять следующие суффиксы.

Таким образом, операция insert позволяет суффиксы не только для подстрок [math]S[i..j][/math], но и сразу для всего суффикса [math]S[i..n][/math].

Суффиксные ссылки

Определение:

Пусть [math]x\alpha[/math] обозначает произвольную строку, где [math]x[/math] — ее первый символ, а [math]\alpha[/math] — оставшаяся подстрока(возможно пустая). Если для внутренней вершины [math]v[/math] с путевой меткой [math]x\alpha[/math] существует другая вершина [math]s(v)[/math] с путевой меткой [math]\alpha[/math], то ссылка из [math]v[/math] в [math]s(v)[/math] называется суффиксной ссылкой.

Лемма 3. Существование суффиксных ссылок

Лемма:

Для любой внутренней вершины [math]v[/math] суффиксного дерева существует суффиксная ссылка, ведущая в некоторую внутреннюю вершину [math]u[/math].

Доказательство:

[math]\triangleright[/math]

Рассмотрим внутренную вершину [math]v[/math] с путевой меткой [math]t_i ... t_j[/math]. Так как эта вершина внутренняя, ее путевая метка ветвится справа в исходной строке. Тогда очевидно подстрока [math]t_{i+1} ... t_j[/math] тоже ветвится справа в исходной строке, и ей соответствует некоторая внутренняя вершина [math]u[/math]. По определению суффиксная ссылка вершины [math]v [/math] ведет в [math] u[/math]

[math]\triangleleft[/math]

Построение суффиксных ссылок

Заметим что в процессе построения суффиксного дерева уже построенные суффиксные ссылки никак не изменяются. Опишем процесс построения суффиксной ссылки для новой созданной внутренней вершины. Пусть в результате очередного продления была создана новая внутренняя вершина [math]v [/math] с путевой меткой [math]t_i ... t_j[/math]. Перейдем к следущему шагу текущей фазы, на котором в дерево будет добавлен суффикс [math]t_{i + 1} ... t_j[/math] соответствующий вершине [math]u[/math] (возможно до продления суффикс оканчивался на ребре, но в этом случае по рассуждениям аналогичным Лемме 1 будет создана новая внутрення вершина). По определению суффиксная ссылка из вершины [math]v[/math] ведет в [math]u[/math].

Использование суффиксных ссылок

Опишем как искать концы суффиксов в дереве, которые нужно продлить. Пусть мы только что продлили суффикс [math]t_i ... t_j[/math]. Найдем с помощью построенных ссылок конец суффикса [math]t_{i + 1} ... t_j[/math]. Пройдем вверх по дереву от конца суффикса [math]t_i ... t_j[/math] до ближайшей внутренней вершины [math]v[/math]. Ей соответствует некоторая подстрока [math]t_i ... t_k [/math]. У вершины [math]v[/math] есть суффиксная ссылка, так как ссылка для новой внутренней вершины строится внутри фазы ее создания. Пусть суффиксная ссылка ведет в вершину [math]u[/math], которой соответствует подстрока [math]t_{i + 1} ... t_k[/math]. Теперь пройдем от вершины [math]u[/math] пройдем вниз по дереву, читая текст [math]t_{k + 1} ... t_j[/math], и придем к концу суффикса [math]t_{i + 1} ... t_j[/math].

Оценка числа переходов

Определение:

Глубиной вершины [math]d(v)[/math] назовем число ребер на пути от корня до вершины [math]v[/math]

Лемма 4.

Лемма:

При переходе по суффиксной ссылке глубина уменьшается не более чем на 1.

Доказательство:

[math]\triangleright[/math]

Пусть мы переходим из вершины [math] v [/math] с путевой меткой [math]t_i ... t_j[/math] по суффиксной ссылке в вершину [math] u [/math] с путевой меткой [math]t_{i + 1} ... t_j[/math] Определим множество [math] A [/math] как множество вершин на пути от корня до [math] u [/math], исключая корень. Множество [math] B [/math] определим как множество вершин на пути от корня до [math] v [/math], исключая корень. Если длина первого ребра на пути от корня до [math] v [/math] равна единице, то выкинем из множества [math]B[/math] вершину, в которую ведет это ребро. Итого по построению получаем: [math]|A| = d(u)[/math], [math]|B| \ge d(v) - 1[/math]. Теперь заметим, что суффиксная ссылка из любой вершины множества [math]B[/math] ведет в некоторую вершину множества [math] A[/math], и очевидно суффиксные ссылки из разных вершин ведут в разные вершины, поэтому [math]|A| \ge |B|[/math], а значит [math]d(u) \ge d(v) - 1[/math]

[math]\triangleleft[/math]

Лемма 5.

Лемма:

Число переходов по ребрам внутри фазы номер [math]i[/math] не превышает [math]4i[/math]

Доказательство:

[math]\triangleright[/math]

Оценим количество переходов по ребрам при поиске конца суффикса. Переход до ближайшей внутренней вершины уменьшает высоту на 1. Переход по суффиксной ссылке уменьшает высоту не более чем на 1 (по Лемме 4). Значит в течение одной фазы вверх мы переходим не более [math] 2i [/math] раз. Но внутри одной фазы начальная глубина не меньше конечной (так как длины суффиксов убывают до 1), поэтому вниз мы могли пройти не более [math] 2i [/math] ребер. Итого получаем оценку [math] 4i [/math]

[math]\triangleleft[/math]

Псевдокод

 string s;
 int n;

 struct node {
   int l, r, par, link;
   map<char,int> next;

   node (int l=0, int r=0, int par=-1)
     : l(l), r(r), par(par), link(-1) {}
   int len()  {  return r - l;  }
   int &get (char c) {
     if (!next.count(c))  next[c] = -1;
     return next[c];
   }
 };
 node t[MAXN];
 int sz;

 struct state {
   int v, pos;
   state (int v, int pos) : v(v), pos(pos)  {}
 };
 state ptr (0, 0);

 state go (state st, int l, int r) {
   while (l < r)
     if (st.pos == t[st.v].len()) {
       st = state (t[st.v].get( s[l] ), 0);
       if (st.v == -1)  return st;
     }
     else {
       if (s[ t[st.v].l + st.pos ] != s[l])
         return state (-1, -1);
       if (r-l < t[st.v].len() - st.pos)
         return state (st.v, st.pos + r-l);
       l += t[st.v].len() - st.pos;
       st.pos = t[st.v].len();
     }
   return st;
 }

 int split (state st) {
   if (st.pos == t[st.v].len())
     return st.v;
   if (st.pos == 0)
     return t[st.v].par;
   node v = t[st.v];
   int id = sz++;
   t[id] = node (v.l, v.l+st.pos, v.par);
   t[v.par].get( s[v.l] ) = id;
   t[id].get( s[v.l+st.pos] ) = st.v;
   t[st.v].par = id;
   t[st.v].l += st.pos;
   return id;
 }

 int get_link (int v) {
   if (t[v].link != -1)  return t[v].link;
   if (t[v].par == -1)  return 0;
   int to = get_link (t[v].par);
   return t[v].link = split (go (state(to,t[to].len()), t[v].l + (t[v].par==0), t[v].r));
 }

 void tree_extend (int pos) {
   for(;;) {
     state nptr = go (ptr, pos, pos+1);
     if (nptr.v != -1) {
       ptr = nptr;
       return;
     }

     int mid = split (ptr);
     int leaf = sz++;
     t[leaf] = node (pos, n, mid);
     t[mid].get( s[pos] ) = leaf;

     ptr.v = get_link (mid);
     ptr.pos = t[ptr.v].len();
     if (!mid)  break;
   }
 }

 void build_tree() {
   sz = 1;
   for (int i=0; i<n; ++i)
     tree_extend (i);
 }

Итоговая линейная оценка

Оценим время работы алгоритма при использовании всех вышеперечисленных эвристик.

Все неявные продления листов суммарно можно выполнить за [math]O(n)[/math] (по Лемме 1) По Лемме 2 алгоритм делает не более [math]2n[/math] явных продлений. При использовании суффиксных ссылок, как показано в Лемме 5 время на продление равно константе плюс время пропорциональное числу ребер, пройденных при спуске по дереву. Оценим суммарное число таких переходов по ребрам. Первое явное продолжение в любой фазе (кроме первой) начинается с продолжения, которое было последним явным в предыдущей фазе. Поэтому текущаю вершинная глубина не изменяется при переходе к следущей фазе. Как было показано в Лемме 5, каждое продление представляет собой переход не более чем на 2 единицы глубины вверх, а затем несколько переходов вниз, каждый из которых увеличивает глубину на 1. Так как максимальная глубина не превосходит [math]n[/math], а количество явных продлений не превышает [math]2n[/math], то по рассуждениям аналогичным Лемме 5 суммарное число таких переходов имеет порядок [math]O(n)[/math]

Источники

• Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.
• Реализация алгоритма Укконена
• Построение суффиксного дерева: алгоритм Укконена

См. также

• Алгоритм МакКрейта
• Алгоритм Фарача