Симуляция одним распределением другого — различия между версиями
Proshev (обсуждение | вклад) |
|||
| Строка 28: | Строка 28: | ||
==Общий случай== | ==Общий случай== | ||
| − | [[Файл:Sim pic1.JPG| | + | [[Файл:Sim pic1.JPG|170px|left|thumb|В распределении q количество элементарных исходов равно 2]] |
Допустим у нас есть распределение <tex>p.</tex> Нам нужно получить распределение <tex>q</tex>. | Допустим у нас есть распределение <tex>p.</tex> Нам нужно получить распределение <tex>q</tex>. | ||
| Строка 34: | Строка 34: | ||
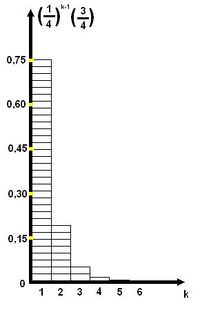
Проводим эксперимент: если попадаем в область пересекающуюся с <tex> q_1 </tex> и <tex> q_2,</tex> то увеличиваем ее и повторяем эксперимент. На рисунке слева красным обозначенно распределение <tex> q. </tex> Вероятность того, что на этом шаге эксперимент не закончится {{---}} <tex>\frac{1}{k}.</tex> Математическое ожидание количества экспериментов {{---}} <tex> \frac{k}{k-1}, max(\frac{k}{k-1}) = 2 (</tex>при <tex>k = 2) </tex> | Проводим эксперимент: если попадаем в область пересекающуюся с <tex> q_1 </tex> и <tex> q_2,</tex> то увеличиваем ее и повторяем эксперимент. На рисунке слева красным обозначенно распределение <tex> q. </tex> Вероятность того, что на этом шаге эксперимент не закончится {{---}} <tex>\frac{1}{k}.</tex> Математическое ожидание количества экспериментов {{---}} <tex> \frac{k}{k-1}, max(\frac{k}{k-1}) = 2 (</tex>при <tex>k = 2) </tex> | ||
| − | [[Файл:Sim pic2.JPG| | + | [[Файл:Sim pic2.JPG|170px|right|thumb|Количество элементарных исходов распределения q равно n]] |
Теперь рассмотрим случай, когда все элементарные исходы <tex>p_i</tex> по-прежнему равновероятны <tex>(p_i = \frac{1}{k}),</tex>а количество элементарных исходов распределения <tex>q</tex> равно <tex>n (\sum\limits_{j=1}^{n}q_j = 1).</tex> Повторим эксперимент <tex> t </tex> раз. | Теперь рассмотрим случай, когда все элементарные исходы <tex>p_i</tex> по-прежнему равновероятны <tex>(p_i = \frac{1}{k}),</tex>а количество элементарных исходов распределения <tex>q</tex> равно <tex>n (\sum\limits_{j=1}^{n}q_j = 1).</tex> Повторим эксперимент <tex> t </tex> раз. | ||
| Строка 41: | Строка 41: | ||
Отрезок разбился на <tex> k^t </tex> отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов <tex> \approx 2t </tex> | Отрезок разбился на <tex> k^t </tex> отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов <tex> \approx 2t </tex> | ||
| − | [[Файл:Sim pic3.JPG| | + | [[Файл:Sim pic3.JPG|170px|left|thumb]] |
<tex>p_i, \sum\limits_{i}p_i = 1,</tex> | <tex>p_i, \sum\limits_{i}p_i = 1,</tex> | ||
Версия 16:56, 17 июня 2014
<wikitex>
Содержание
Распределение
Распределение — одно из основных понятий в теории вероятностей и математической статистике. Распределение вероятностей какой-либо случайной величины задается в простейшем случае указанием возможных значений этой величины и соответствующих им вероятностей, в более сложных — т. н. функцией распределения или плотностью вероятности.
Примеры распределений
- Биномиальное распределение
- Нормальное распределение
- Равномерное распределение
Симуляция распределений
Для того, чтобы создать необходимое распределение вероятностей, достаточно иметь последовательность независимых случайных величин типа "честной монеты". Например, для создания схемы с двумя исходами $A_1$ и $A_2$:
можно из датчика случайных двоичных величин получить два результата "честой монеты" $\delta_1$ и $\delta_2$ и, например, при $\delta_1 = \delta_2 = 1$ выработать исход $A_2$, а в остальных случаях $A_1$. Аналогично для схемы с четырьмя исходами
можно получить четыре результата "честной монеты" $\delta_1$ $,$ $\delta_2$ $,$ $\delta_3$ $,$ $\delta_4$ и любым способом сопоставить трём из 16 возможных наборов исход $A_1$, одному $-$ $A_2$, восьми $-$ $A_3$, четырём $-$ $A_4$. Если же вероятности исходов не кратны $2^{-k}$, можно применить два различных варианта действий.
- Можно приблизить вероятности двоичными дробями (с любой точностью), далее работать с полученными приближёнными значениями
- Пусть все вероятности $n_i$ $-$ дроби со знаменателем $r$. Найдём $k$, для которого $r < 2^k$. Предложим схему с $k$ результатами "честной монеты", в которой $r$ наборов используются для выработки случайного исхода, а остальные $2^{k}-r$ наборов объявляются "неудачными" и требуют повторного эксперимента (пока не встретится удачный). Чем выше доля полезных исходов равная $r2^{-k}$, тем схема будет эффективнее.
Количество результатов "честной монеты" $\lambda$, которые необходимы для формирования случайного исхода, $-$ это случайная величина. Её математическое ожидание:
Можно сделать схему более экономной, используя свойство датчика случайных чисел формировать не отдельные результаты "честной монеты", а целые наборы их, например в виде числа, равномерно распределённого в $[0, 1]$. Образуем по данному набору вероятностей $p_i$ накопленные суммы $s_i$: $s_0 = 0; s_i = s_{i-1} + p_i, i > 0$. Случайный исход будет вырабатываться так: по полученному из датчика случайному числу $\gamma$ определяется такой индекс $i$, для которого $s_{i-1} < \gamma \le s_i$. Найденное значение индекса $i$ и определяет исход $A_i$.
Индекс $i$ можно определять непосредственно просмотром $s_i$ подряд. Если $k$ велико, можно применять специальные приёмы ускоренного поиска, например, деление множества индексов примерно пополам.
Общий случай
Допустим у нас есть распределение Нам нужно получить распределение .
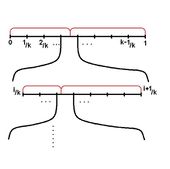
Для начала рассмотрим случай, когда все а в распределении количество элементарных исходов равно Проводим эксперимент: если попадаем в область пересекающуюся с и то увеличиваем ее и повторяем эксперимент. На рисунке слева красным обозначенно распределение Вероятность того, что на этом шаге эксперимент не закончится — Математическое ожидание количества экспериментов — при
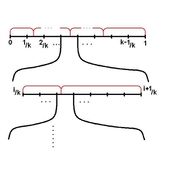
Теперь рассмотрим случай, когда все элементарные исходы по-прежнему равновероятны а количество элементарных исходов распределения равно Повторим эксперимент раз.
Отрезок разбился на отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов
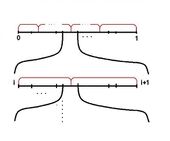
Берем , и пусть оно максимальной длины. Проводим экспериментов. все остальные еще меньше. Суммарная длина отрезков не больше Нужно
Вывод: из любого исходного распределения можно получить любое нужное нам распределение.
</wikitex>
См. также
Литература
- Боровков А.А. Математическая статистика: оценка параметров, проверка гипотез. - М., Физматлит, 1984.
- Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн - Алгоритмы. Построение и анализ 1244c.
- Романовский И.В. Дискретный анализ