Теорема Понтрягина-Куратовского — различия между версиями
м (Добавлены категории) |
(→Разбор случаев взаимного положения a, b, c, d, u1, u2, v1, v2) |
||
| Строка 1: | Строка 1: | ||
| + | {{Теорема | ||
| + | |statement = | ||
| + | Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных <tex> K_{5} </tex>, и не содержит подграфов, гомеоморфных <tex> K_{3, 3} </tex> . | ||
| + | |proof = | ||
| + | === Необходимость === | ||
| + | Необходимость условия очевидна. | ||
| + | === Достаточность === | ||
| + | От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex>. Пусть <tex> G </tex> - такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. | ||
| + | ==== G связен ==== | ||
| + | Если <tex> G </tex> не связен, то его компоненты связности планарны и, следовательно, сам граф <tex> G </tex> планарен. | ||
| + | ==== G - обыкновенный граф ==== | ||
| + | В самом деле, пусть в графе <tex> G </tex> есть петля или кратное ребро <tex> e </tex>. Тогда граф <tex> G - e </tex> планарен. Добавляя ребро <tex> e </tex> к графу <tex> G - e </tex> получим, что граф <tex> G </tex> он планарен. | ||
| + | ==== G - блок ==== | ||
| + | Пусть, от противного, в графе есть точка сочленения <tex> v </tex>. Через <tex> G_1 </tex> обозначим подграф графа <tex> G </tex>, порождённый вершинами одной из компонент связности графа <tex> G - v</tex> и вершинной <tex> v </tex>, а через | ||
| + | <tex> G_2 </tex> подграф графа <tex> G </tex>, порождённый вершинами остальных компонент связности графа <tex> G - v </tex> и вершиной <tex> v </tex>. (рис. 1) | ||
| + | |||
| + | |||
==== Разбор случаев взаимного положения ''a, b, c, d, u1, u2, v1, v2'' ==== | ==== Разбор случаев взаимного положения ''a, b, c, d, u1, u2, v1, v2'' ==== | ||
Рассмотрим 2 случая. | Рассмотрим 2 случая. | ||
| Строка 69: | Строка 86: | ||
Таким образом, доказано, что в графе G имеется подграф, гомеоморфный <tex>K_{3,3}</tex> или <tex>K_5</tex>, что противоречит нашему первому предположению.<br> | Таким образом, доказано, что в графе G имеется подграф, гомеоморфный <tex>K_{3,3}</tex> или <tex>K_5</tex>, что противоречит нашему первому предположению.<br> | ||
| + | }} | ||
==Литература== | ==Литература== | ||
Версия 04:08, 20 октября 2010
| Теорема: |
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных , и не содержит подграфов, гомеоморфных . |
| Доказательство: |
СодержаниеНеобходимостьНеобходимость условия очевидна. ДостаточностьОт противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных или . Пусть - такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. G связенЕсли не связен, то его компоненты связности планарны и, следовательно, сам граф планарен. G - обыкновенный графВ самом деле, пусть в графе есть петля или кратное ребро . Тогда граф планарен. Добавляя ребро к графу получим, что граф он планарен. G - блокПусть, от противного, в графе есть точка сочленения . Через обозначим подграф графа , порождённый вершинами одной из компонент связности графа и вершинной , а через подграф графа , порождённый вершинами остальных компонент связности графа и вершиной . (рис. 1)
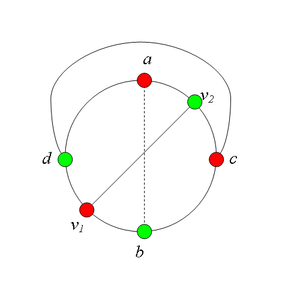
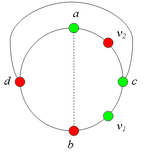
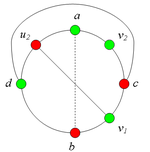
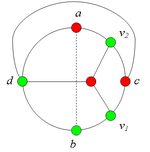
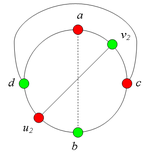
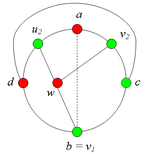
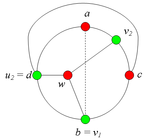
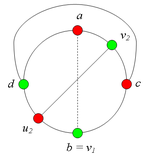
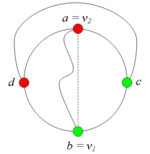
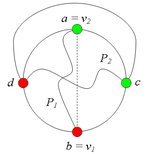
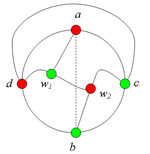
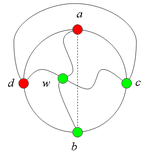
Разбор случаев взаимного положения a, b, c, d, u1, u2, v1, v2Рассмотрим 2 случая. 1. Пусть пара вершин и является -разделяющей. 2. Пусть пара вершин и не является -разделяющей. 2.1. Пусть и лежат на , т.е. и (рис. 2). 2.1.1 Пусть лежит на . 2.1.2. Пусть . 2.1.3. Пусть лежит на . Теперь рассмотрим случаи, когда хотя бы одна из вершин и не лежит на . Без ограничения общности будем считать, что это вершина , т.е (поскольку лежит на ). 2.2. Пусть . 2.2.1. Пусть лежит на . 2.2.2. Пусть . 2.2.3. Пусть лежит на . 2.3. Пусть (рис. 9). 2.3.1. Пусть цепи и имеют более одной общей точки. 2.3.2. Пусть цепи и имеют точно одну общую точку . |
Литература
- Асанов М,, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы