Расширяемое хеширование — различия между версиями
Шубин (обсуждение | вклад) (Новая страница: «'''Метод расширяемого хеширования''' (''extendable hashing'') представляет собой изящный вариант осн...») |
Шубин (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | '''Метод расширяемого хеширования''' ('' | + | '''Метод расширяемого хеширования''' (англ. ''extendible hashing'') предусматривает изменение размеров блоков по мере роста базы данных, но это компенсируется оптимальным использованием места. Т.к. за один раз разбивается не более одного блока, накладные расходы достаточно малы |
| + | == Алгоритм == | ||
| + | Посмотрим, как работает алгоритм, на примере заполнения гипотетической хеш-таблицы. Первоначально в таблице имеется одна группа. Предположим, что каждая группа будет содержать 10 хеш-значений и номер записи каждого хеш-значения, чтобы ее можно было извлечь. Обратите внимание, что мы не помещаем в группы сами ключи. При использовании 32-разрядных хеш-значений, маловероятно, чтобы два ключа хешировались в одно и то же значение. (Фактически это будет происходить настолько редко, что для проверки ключей можно извлечь саму запись без заметного замедления всего процесса. Естественно, при этом предполагается, что используемая хеш-функция успешно справляется с рандомизацией.) | ||
| − | ''' | + | Начнем вставлять в таблицу хеш-значения вместе с номерами их записей. При наличии только одной группы их можно вставить только в одно место, поэтому после 10 вставок группа заполняется. Разобьем заполненную группу на две группы одинаковых размеров и повторим вставку всех элементов исходной группы в две новые группы. Причем все элементы, которые завершаются нулевым разрядом, поместим в одну группу, а завершающиеся единичным разрядом - в другую. Эти две группы имеют так называемую разрядную глубину (англ. ''bit-depth''), равную одному разряду. Теперь при каждой вставке пары хеш-значение/номер записи она будет помещаться в первую или во вторую группу, в зависимости от последнего разряда хеш-значения. |
| − | + | ||
| − | + | Со временем мы заполним еще одну группу. Предположим, что это группа, в которую мы вставляли все хеш-значения, завершающиеся 0. Снова разобьем группу на две отдельные группы. На этот раз все элементы, хеш-значения которых заканчиваются двумя нулевыми разрядами, т.е. 00, будут помещаться в первую группу, а завершающиеся разрядами 10 - во вторую группу. Обе группы имеют разрядную глубину, равную 2. Поэтому для определения места вставки необходимо проверять два младших разряда хеш-значения. Теперь у нас имеются три группы: в первую вставляются элементы, завершающиеся разрядами 00, во вторую -разрядами 10, а в третью - просто 1. | |
| − | + | ||
| − | + | Предположим, что мы продолжаем вставку и заполняем группу 10. Мы снова разбиваем заполненную группу на две и повторяем вставку ее элементов в две новые группы. На этот раз две новые группы будут принимать элементы, завершающиеся разрядами 010 и 110. Таким образом, теперь у нас имеются четыре группы: одна с разрядной глубиной, равной 1, в которую выполняется вставка хеш-значений, завершающихся 1, одна с разрядной глубиной равной 2, содержащая хеш-значения, которые завершаются разрядами 00, и две группы с разрядной глубиной, равной 3, которые предназначены для хеш-значений, завершающихся разрядами 010 и 110. | |
| − | + | ||
| − | + | Для поддержания отображения того, какие хеш-значения помещаются в те или иные группы, используется структура, называемая каталогом (англ. ''catalogue''). По существу каталог содержит список всех возможных окончаний групп и связных с ними номеров групп. Вместо того чтобы поддерживать какой-либо причудливый набор значений разрядной глубины и номеров групп, выбранный методом проб и ошибок, каталог поддерживает собственное значение разрядной глубины, равное максимальной разрядной глубине группы, и имеет ячейку для каждого значения этой разрядной глубины. | |
| − | + | ||
| + | В рассмотренном нами примере максимальная разрядная глубина группы была равна 3, поэтому разрядная глубина каталога также равна этому значению. Три разряда позволяют образовать восемь комбинаций разрядов: 000, 001, 010, 011, 100, 101, 110 и 111. Все комбинации, которые завершаются 1 (т.е. вторая, четвертая, шестая и восьмая), указывают на одну и ту же группу, принимающую элементы, хеш-значения которых завершаются 1. Аналогично, записи каталога для значений 000 и 100 указывают на одну и ту же группу, в которую помещаются элементы с хеш-значениями, завершающимися разрядами 00. | ||
| + | |||
| + | [[Файл:7_1.png|400px|мини|Вставка в расширяемую хеш-таблицу]] | ||
| + | |||
| + | Однако эта схема не учитывает ряд особенностей. Две записи каталога, которые указывают на группу для элементов, хеш-значения которых завершаются разрядами 00, разделены тремя другими записями. Аналогично единственной группе, принимающей все элементы, хеш-значения которых завершаются 1, соответствуют четыре записи, равномерно распределенные по каталогу. При разбиении группы дополняющие друг друга группы не будут размещаться в каталоге по соседству. Для дальнейших рассуждений было бы проще предположить, что записи каталога, соответствующие одной группе, располагаются по соседству, чтобы при разбиении группы дополняющая первую группа помещалась непосредственно за ней. | ||
| + | |||
| + | |||
| + | Для достижения этого следует инвертировать последние разряды хеш-значения при вычислении индексной записи каталога. Так, например, если хеш-значение завершается разрядами 001, при поиске мы обратимся не к записи 001 каталога, а к записи 100 (4, которая соответствует инвертированному значению 001). В результате использование каталога значительно упрощается. В нашем примере хеш-значения, которые завершаются разрядами 00, помещаются в запись каталога 000 (0) или 001 (1). Хеш-значения, которые завершаются разрядами 010, помещаются в запись каталога 010 (2). Хеш-значения, которые завершаются разрядами 011, помещаются в запись каталога 011 (3). И, наконец, хеш-значения, которые завершаются разрядом 1, помещаются в записи 100, 101, 110 или 111 (4, 5, 6, 7). | ||
| + | |||
| + | Вернемся немного назад, и вставим элементы в пустую хеш-таблицу, как это было сделано ранее. Выполняемые при этом действия показаны на рис. Мы начинаем с каталога только с одной записью с индексом 0 (а). Принято считать, что в подобной ситуации разрядная глубина равна 0. Мы заполняем единственную группу (назовем ее А) и теперь ее нужно разбить. Вначале мы увеличиваем разрядную глубину каталога до 1. Иначе говоря, теперь он будет содержать две записи (b). В результате будут созданы две группы, на первую из которых указывает запись 0 (исходная запись А), а на вторую - запись 1, В (с). Все элементы, хеш-значения которых завершаются разрядом 0, помещаются в группу А, а остальные - в группу В. Снова заполним группу A. Теперь разрядную глубину каталога необходимо увеличить с 1 до 2, чтобы получить четыре группы, доступных для вставки. Перед разделением заполненной группы записи каталога 00 и 01 будут указывать на исходную группу А, а записи 10 и 11 - на группу В (d). Группа А разбивается на группу, которая принимает хеш-значения с окончанием 00 (снова А), и группу, которая принимает хеш-значения с окончанием 10, С. На группу А будет указывать запись 00 каталога, а на группу С - запись 01 (e). И, наконец, группа С (на которую указывает запись 01 каталога) заполняется. Нужно снова увеличить разрядную глубину каталога, на этот раз до трех разрядов. | ||
== См. также == | == См. также == | ||
*[[Хеш-таблица]] | *[[Хеш-таблица]] | ||
| Строка 18: | Строка 30: | ||
*[http://src-code.net/rasshiryaemyj-metod-xeshirovaniya/ http://src-code.net - Расширяемый метод хеширования] | *[http://src-code.net/rasshiryaemyj-metod-xeshirovaniya/ http://src-code.net - Расширяемый метод хеширования] | ||
*Дейт К. Дж., Введение в системы баз данных, 8-е издание.: Пер. с англ. — М.: Издательский дом «Вильямс», 2005. — стр. 1236 | *Дейт К. Дж., Введение в системы баз данных, 8-е издание.: Пер. с англ. — М.: Издательский дом «Вильямс», 2005. — стр. 1236 | ||
| − | [[Категория: Дискретная математика и алгоритмы]] | + | [[Категория: Дискретная математика и алгоритмы]][[Категория: Структуры данных]] |
Версия 23:51, 5 июня 2015
Метод расширяемого хеширования (англ. extendible hashing) предусматривает изменение размеров блоков по мере роста базы данных, но это компенсируется оптимальным использованием места. Т.к. за один раз разбивается не более одного блока, накладные расходы достаточно малы
Алгоритм
Посмотрим, как работает алгоритм, на примере заполнения гипотетической хеш-таблицы. Первоначально в таблице имеется одна группа. Предположим, что каждая группа будет содержать 10 хеш-значений и номер записи каждого хеш-значения, чтобы ее можно было извлечь. Обратите внимание, что мы не помещаем в группы сами ключи. При использовании 32-разрядных хеш-значений, маловероятно, чтобы два ключа хешировались в одно и то же значение. (Фактически это будет происходить настолько редко, что для проверки ключей можно извлечь саму запись без заметного замедления всего процесса. Естественно, при этом предполагается, что используемая хеш-функция успешно справляется с рандомизацией.)
Начнем вставлять в таблицу хеш-значения вместе с номерами их записей. При наличии только одной группы их можно вставить только в одно место, поэтому после 10 вставок группа заполняется. Разобьем заполненную группу на две группы одинаковых размеров и повторим вставку всех элементов исходной группы в две новые группы. Причем все элементы, которые завершаются нулевым разрядом, поместим в одну группу, а завершающиеся единичным разрядом - в другую. Эти две группы имеют так называемую разрядную глубину (англ. bit-depth), равную одному разряду. Теперь при каждой вставке пары хеш-значение/номер записи она будет помещаться в первую или во вторую группу, в зависимости от последнего разряда хеш-значения.
Со временем мы заполним еще одну группу. Предположим, что это группа, в которую мы вставляли все хеш-значения, завершающиеся 0. Снова разобьем группу на две отдельные группы. На этот раз все элементы, хеш-значения которых заканчиваются двумя нулевыми разрядами, т.е. 00, будут помещаться в первую группу, а завершающиеся разрядами 10 - во вторую группу. Обе группы имеют разрядную глубину, равную 2. Поэтому для определения места вставки необходимо проверять два младших разряда хеш-значения. Теперь у нас имеются три группы: в первую вставляются элементы, завершающиеся разрядами 00, во вторую -разрядами 10, а в третью - просто 1.
Предположим, что мы продолжаем вставку и заполняем группу 10. Мы снова разбиваем заполненную группу на две и повторяем вставку ее элементов в две новые группы. На этот раз две новые группы будут принимать элементы, завершающиеся разрядами 010 и 110. Таким образом, теперь у нас имеются четыре группы: одна с разрядной глубиной, равной 1, в которую выполняется вставка хеш-значений, завершающихся 1, одна с разрядной глубиной равной 2, содержащая хеш-значения, которые завершаются разрядами 00, и две группы с разрядной глубиной, равной 3, которые предназначены для хеш-значений, завершающихся разрядами 010 и 110.
Для поддержания отображения того, какие хеш-значения помещаются в те или иные группы, используется структура, называемая каталогом (англ. catalogue). По существу каталог содержит список всех возможных окончаний групп и связных с ними номеров групп. Вместо того чтобы поддерживать какой-либо причудливый набор значений разрядной глубины и номеров групп, выбранный методом проб и ошибок, каталог поддерживает собственное значение разрядной глубины, равное максимальной разрядной глубине группы, и имеет ячейку для каждого значения этой разрядной глубины.
В рассмотренном нами примере максимальная разрядная глубина группы была равна 3, поэтому разрядная глубина каталога также равна этому значению. Три разряда позволяют образовать восемь комбинаций разрядов: 000, 001, 010, 011, 100, 101, 110 и 111. Все комбинации, которые завершаются 1 (т.е. вторая, четвертая, шестая и восьмая), указывают на одну и ту же группу, принимающую элементы, хеш-значения которых завершаются 1. Аналогично, записи каталога для значений 000 и 100 указывают на одну и ту же группу, в которую помещаются элементы с хеш-значениями, завершающимися разрядами 00.
Однако эта схема не учитывает ряд особенностей. Две записи каталога, которые указывают на группу для элементов, хеш-значения которых завершаются разрядами 00, разделены тремя другими записями. Аналогично единственной группе, принимающей все элементы, хеш-значения которых завершаются 1, соответствуют четыре записи, равномерно распределенные по каталогу. При разбиении группы дополняющие друг друга группы не будут размещаться в каталоге по соседству. Для дальнейших рассуждений было бы проще предположить, что записи каталога, соответствующие одной группе, располагаются по соседству, чтобы при разбиении группы дополняющая первую группа помещалась непосредственно за ней.
Для достижения этого следует инвертировать последние разряды хеш-значения при вычислении индексной записи каталога. Так, например, если хеш-значение завершается разрядами 001, при поиске мы обратимся не к записи 001 каталога, а к записи 100 (4, которая соответствует инвертированному значению 001). В результате использование каталога значительно упрощается. В нашем примере хеш-значения, которые завершаются разрядами 00, помещаются в запись каталога 000 (0) или 001 (1). Хеш-значения, которые завершаются разрядами 010, помещаются в запись каталога 010 (2). Хеш-значения, которые завершаются разрядами 011, помещаются в запись каталога 011 (3). И, наконец, хеш-значения, которые завершаются разрядом 1, помещаются в записи 100, 101, 110 или 111 (4, 5, 6, 7).
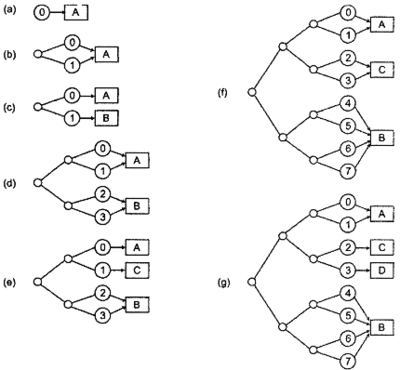
Вернемся немного назад, и вставим элементы в пустую хеш-таблицу, как это было сделано ранее. Выполняемые при этом действия показаны на рис. Мы начинаем с каталога только с одной записью с индексом 0 (а). Принято считать, что в подобной ситуации разрядная глубина равна 0. Мы заполняем единственную группу (назовем ее А) и теперь ее нужно разбить. Вначале мы увеличиваем разрядную глубину каталога до 1. Иначе говоря, теперь он будет содержать две записи (b). В результате будут созданы две группы, на первую из которых указывает запись 0 (исходная запись А), а на вторую - запись 1, В (с). Все элементы, хеш-значения которых завершаются разрядом 0, помещаются в группу А, а остальные - в группу В. Снова заполним группу A. Теперь разрядную глубину каталога необходимо увеличить с 1 до 2, чтобы получить четыре группы, доступных для вставки. Перед разделением заполненной группы записи каталога 00 и 01 будут указывать на исходную группу А, а записи 10 и 11 - на группу В (d). Группа А разбивается на группу, которая принимает хеш-значения с окончанием 00 (снова А), и группу, которая принимает хеш-значения с окончанием 10, С. На группу А будет указывать запись 00 каталога, а на группу С - запись 01 (e). И, наконец, группа С (на которую указывает запись 01 каталога) заполняется. Нужно снова увеличить разрядную глубину каталога, на этот раз до трех разрядов.
См. также
Источники информации
- http://src-code.net - Расширяемый метод хеширования
- Дейт К. Дж., Введение в системы баз данных, 8-е издание.: Пер. с англ. — М.: Издательский дом «Вильямс», 2005. — стр. 1236