Расширяемое хеширование — различия между версиями
Shersh (обсуждение | вклад) м (→Пример) |
Шубин (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
При частом добавлении новых значений в хеш-таблицу может возникнуть ситуация, когда хеш-таблица становится полностью заполненной и требуется перехешировать ее. Но при больших размерах хеш-таблицы это требует большого количества времени. Чтобы решить эту проблему, а также чтобы не выделять много дополнительной памяти можно использовать расширяемое хеширование. | При частом добавлении новых значений в хеш-таблицу может возникнуть ситуация, когда хеш-таблица становится полностью заполненной и требуется перехешировать ее. Но при больших размерах хеш-таблицы это требует большого количества времени. Чтобы решить эту проблему, а также чтобы не выделять много дополнительной памяти можно использовать расширяемое хеширование. | ||
== Структура и алгоритм == | == Структура и алгоритм == | ||
| − | '''Метод расширяемого хеширования''' (англ. ''extendible hashing'') заключается в том, что хеш-таблица представлена как каталог (англ. ''directory''), а каждая ячейка будет указывать на емкость (англ. ''bucket'') которая имеет определенную вместимость (англ. capacity). Сама хеш-таблица будет иметь глобальную глубину (англ. ''global depth''), а каждая из емкостей имеет локальную глубину (англ. ''local depth''). | + | '''Метод расширяемого хеширования''' (англ. ''extendible hashing'') заключается в том, что хеш-таблица представлена как каталог (англ. ''directory''), а каждая ячейка будет указывать на емкость (англ. ''bucket'') которая имеет определенную вместимость (англ. capacity). Сама хеш-таблица будет иметь глобальную глубину (англ. ''global depth''), а каждая из емкостей имеет локальную глубину (англ. ''local depth''). Глобальная глубина показывает сколько последних бит будут использоваться для того чтобы определить в какую емкость следует заносить значения. А из разницы локальной глубины и глобальной глубины можно понять сколько ячеек каталога ссылаются на емкость. Это можно показать формулой <tex>K = 2 </tex><sup><tex>G-L</tex></sup> где <tex>G</tex> — глобальная глубина, а <tex>L</tex> — локальная глубина. Если емкость куда следует положить значение переполнена, то смотрим на локальную глубину емкости. Если она меньше чем глобальная глубина то значит на емкость есть несколько указателей и нам достаточно перехешировать ее, разделив при этом на две и занести значения в новые две емкости увеличив у этих емкостей локальную глубину на <tex>1</tex>. Если же локальная глубина была равна глобальной то мы увеличиваем глобальную глубину на <tex>1</tex>, удваивая при этом количество ячеек, количество указателей на емкости, а также увеличиваем количество последних бит по которым мы распределяем значения. Далее локальная глубина переполненной емкости становится меньше и мы знаем что дальше делать. |
==Пример== | ==Пример== | ||
Рассмотрим алгоритм на примере. | Рассмотрим алгоритм на примере. | ||
| − | Пусть у нас есть некий каталог со своими указателями и мы хотим добавить значения <tex>9, 20, 26</tex> (см. рис1) где <tex>G</tex> — глобальная глубина, <tex>l1, l2, l3, l4</tex> — локальные глубины емкостей, а вместимость емкостей равна <tex>3</tex>. Рассмотрим значение <tex>9</tex>. В двоичном коде оно равно <tex>1001</tex>. Окончание <tex>01</tex> соответствует второй ячейке значит смотрим на вторую емкость. В ней есть свободное место и мы просто помещаем <tex>9</tex> в нее (см. рис2). Далее идет значение <tex>20</tex>. В двоичном виде оно представляется как <tex>10100</tex>. Это значение оканчивается на <tex>00</tex> и должно пойти в первую емкость, но первая емкость полностью заполнена. Следовательно мы смотрим на <tex>l1</tex>. <tex>l1 = G</tex> а значит мы должны удвоить количество ячеек каталога, увеличить глобальную глубину, затем увеличить количество последних бит по которым мы раскидываем значения на <tex>1</tex> и перехешировать первую емкость, разделив ее на две, увеличив локальную глубину и разместив значения по новым емкостям (см. рис3). Теперь рассмотрим последнее число <tex>26</tex>. Его двоичное представление — <tex>11010</tex>. Последние <tex>3</tex> бита соответствуют третьей емкости, но она также полностью заполнена как и во втором случае, но ее локальная глубина меньше чем глобальная а следовательно нам надо только перехешировать емкость и | + | Пусть у нас есть некий каталог со своими указателями и мы хотим добавить значения <tex>9, 20, 26</tex> (см. рис1) где <tex>G</tex> — глобальная глубина, <tex>l1, l2, l3, l4</tex> — локальные глубины емкостей, а вместимость емкостей равна <tex>3</tex>. Рассмотрим значение <tex>9</tex>. В двоичном коде оно равно <tex>1001</tex>. Окончание <tex>01</tex> соответствует второй ячейке значит смотрим на вторую емкость. В ней есть свободное место и мы просто помещаем <tex>9</tex> в нее (см. рис2). Далее идет значение <tex>20</tex>. В двоичном виде оно представляется как <tex>10100</tex>. Это значение оканчивается на <tex>00</tex> и должно пойти в первую емкость, но первая емкость полностью заполнена. Следовательно мы смотрим на <tex>l1</tex>. <tex>l1 = G</tex> а значит мы должны удвоить количество ячеек каталога, увеличить глобальную глубину, затем увеличить количество последних бит по которым мы раскидываем значения на <tex>1</tex> и перехешировать первую емкость, разделив ее на две, увеличив локальную глубину и разместив значения по новым емкостям (см. рис3). Теперь рассмотрим последнее число <tex>26</tex>. Его двоичное представление — <tex>11010</tex>. Последние <tex>3</tex> бита соответствуют третьей емкости, но она также полностью заполнена как и во втором случае, но ее локальная глубина меньше чем глобальная а следовательно нам надо только перехешировать емкость, разделив ее на две, увеличив локальную глубину и разместив значения по новым емкостям (см. рис4). |
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
Версия 22:57, 6 июня 2015
При частом добавлении новых значений в хеш-таблицу может возникнуть ситуация, когда хеш-таблица становится полностью заполненной и требуется перехешировать ее. Но при больших размерах хеш-таблицы это требует большого количества времени. Чтобы решить эту проблему, а также чтобы не выделять много дополнительной памяти можно использовать расширяемое хеширование.
Структура и алгоритм
Метод расширяемого хеширования (англ. extendible hashing) заключается в том, что хеш-таблица представлена как каталог (англ. directory), а каждая ячейка будет указывать на емкость (англ. bucket) которая имеет определенную вместимость (англ. capacity). Сама хеш-таблица будет иметь глобальную глубину (англ. global depth), а каждая из емкостей имеет локальную глубину (англ. local depth). Глобальная глубина показывает сколько последних бит будут использоваться для того чтобы определить в какую емкость следует заносить значения. А из разницы локальной глубины и глобальной глубины можно понять сколько ячеек каталога ссылаются на емкость. Это можно показать формулой где — глобальная глубина, а — локальная глубина. Если емкость куда следует положить значение переполнена, то смотрим на локальную глубину емкости. Если она меньше чем глобальная глубина то значит на емкость есть несколько указателей и нам достаточно перехешировать ее, разделив при этом на две и занести значения в новые две емкости увеличив у этих емкостей локальную глубину на . Если же локальная глубина была равна глобальной то мы увеличиваем глобальную глубину на , удваивая при этом количество ячеек, количество указателей на емкости, а также увеличиваем количество последних бит по которым мы распределяем значения. Далее локальная глубина переполненной емкости становится меньше и мы знаем что дальше делать.
Пример
Рассмотрим алгоритм на примере.
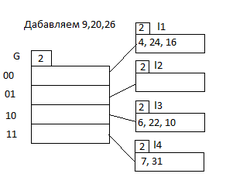
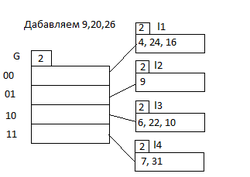
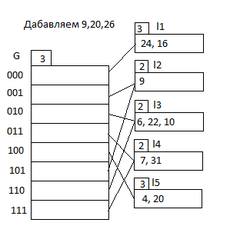
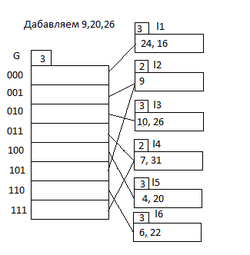
Пусть у нас есть некий каталог со своими указателями и мы хотим добавить значения (см. рис1) где — глобальная глубина, — локальные глубины емкостей, а вместимость емкостей равна . Рассмотрим значение . В двоичном коде оно равно . Окончание соответствует второй ячейке значит смотрим на вторую емкость. В ней есть свободное место и мы просто помещаем в нее (см. рис2). Далее идет значение . В двоичном виде оно представляется как . Это значение оканчивается на и должно пойти в первую емкость, но первая емкость полностью заполнена. Следовательно мы смотрим на . а значит мы должны удвоить количество ячеек каталога, увеличить глобальную глубину, затем увеличить количество последних бит по которым мы раскидываем значения на и перехешировать первую емкость, разделив ее на две, увеличив локальную глубину и разместив значения по новым емкостям (см. рис3). Теперь рассмотрим последнее число . Его двоичное представление — . Последние бита соответствуют третьей емкости, но она также полностью заполнена как и во втором случае, но ее локальная глубина меньше чем глобальная а следовательно нам надо только перехешировать емкость, разделив ее на две, увеличив локальную глубину и разместив значения по новым емкостям (см. рис4).
Использование
Чаще всего расширяемое хеширование используется в базах данных т.к. БД могут быть крайне большими и перехеширование всей БД займет продолжительное время при этом лишая пользователей доступа к БД. А при использовании расширяемого хеширования перехешировать придется только малые группы, что не сильно замедлит работу БД.
См. также
Источники информации
- Бакнелл Джулиан — Фундаментальные алгоритмы и структуры данных в Delphi — стр. 50.
- Дейт К. Дж. — Введение в системы баз данных, 8-е издание.: Пер. с англ. — М.: Издательский дом «Вильямс», 2005. — стр. 1236.