Алгоритм Флойда — различия между версиями
Melnik (обсуждение | вклад) (Картинки) |
|||
| Строка 16: | Строка 16: | ||
Обозначим длину кратчайшего пути между вершинами <tex> u </tex> и <tex> v </tex>, содержащего, помимо <tex>u</tex> и <tex>v</tex>, только вершины из множества <tex> \{ 1 .. i \} </tex> как <tex>d_{uv}^{(i)}</tex>, <tex>d_{uv}^{(0)} = \omega_{uv}</tex>. | Обозначим длину кратчайшего пути между вершинами <tex> u </tex> и <tex> v </tex>, содержащего, помимо <tex>u</tex> и <tex>v</tex>, только вершины из множества <tex> \{ 1 .. i \} </tex> как <tex>d_{uv}^{(i)}</tex>, <tex>d_{uv}^{(0)} = \omega_{uv}</tex>. | ||
| − | На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер {{---}} <tex> i </tex>) и для всех пар вершин <tex>u</tex> и <tex>v</tex> вычислять <tex> d_{uv}^{(i)} = min(d_{uv}^{(i-1)}, d_{ui}^{(i-1)} + d_{iv}^{(i-1)}) </tex>. То есть, если кратчайший путь из <tex>u</tex> в <tex>v</tex>, содержащий только вершины из множества <tex> \{ 1 .. i \} </tex>, проходит через вершину <tex>i</tex>, то кратчайшим путем из <tex> u </tex> в <tex> v </tex> является кратчайший путь из <tex> u </tex> в <tex> i </tex>, объединенный с кратчайшим путем из <tex> i </tex> в <tex> v </tex>. В противном случае, когда этот путь не содержит вершины <tex> i </tex>, кратчайший путь из <tex>u</tex> в <tex>v</tex>, содержащий только вершины из множества <tex> \{ 1 .. i \} </tex> является кратчайшим путем из <tex>u</tex> в <tex>v</tex>, содержащим только вершины из множества <tex> \{ 1 .. i-1 \} </tex>. | + | На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер {{---}} <tex> i </tex>) и для всех пар вершин <tex>u</tex> и <tex>v</tex> вычислять <tex> d_{uv}^{(i)} = \min(d_{uv}^{(i-1)}, d_{ui}^{(i-1)} + d_{iv}^{(i-1)}) </tex>. То есть, если кратчайший путь из <tex>u</tex> в <tex>v</tex>, содержащий только вершины из множества <tex> \{ 1 .. i \} </tex>, проходит через вершину <tex>i</tex>, то кратчайшим путем из <tex> u </tex> в <tex> v </tex> является кратчайший путь из <tex> u </tex> в <tex> i </tex>, объединенный с кратчайшим путем из <tex> i </tex> в <tex> v </tex>. В противном случае, когда этот путь не содержит вершины <tex> i </tex>, кратчайший путь из <tex>u</tex> в <tex>v</tex>, содержащий только вершины из множества <tex> \{ 1 .. i \} </tex> является кратчайшим путем из <tex>u</tex> в <tex>v</tex>, содержащим только вершины из множества <tex> \{ 1 .. i-1 \} </tex>. |
=== Код (в первом приближении) === | === Код (в первом приближении) === | ||
| − | + | <tex>d^{(0)}_{uv} = w</tex> | |
| − | + | '''for''' i = 1 '''to''' n | |
| − | + | '''for''' u = 1 '''to''' n | |
| − | + | '''for''' v = 1 '''to''' n | |
| − | + | <tex> d^{(i)}_{uv} = \min(d^{(i - 1)}_{uv}, d^{(i - 1)}_{ui} + d^{(i - 1)}_{iv}) </tex> | |
| − | |||
| − | |||
В итоге получаем, что матрица <tex> d^{(n)} </tex> и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества <tex> \{ 1..n \} </tex>, что есть попросту все вершины графа. Такая реализация работает за <tex> \Theta(n^3) </tex> времени и использует <tex> \Theta(n^3) </tex> памяти. | В итоге получаем, что матрица <tex> d^{(n)} </tex> и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества <tex> \{ 1..n \} </tex>, что есть попросту все вершины графа. Такая реализация работает за <tex> \Theta(n^3) </tex> времени и использует <tex> \Theta(n^3) </tex> памяти. | ||
=== Код (окончательный) === | === Код (окончательный) === | ||
| − | Утверждается, что можно избавиться от одной размерности в массиве <tex> d </tex>, т.е. использовать двумерный массив <tex>d_{uv}</tex>. В процессе работы алгоритма поддерживается инвариант <tex>\rho(u, v) \ | + | Утверждается, что можно избавиться от одной размерности в массиве <tex> d </tex>, т.е. использовать двумерный массив <tex>d_{uv}</tex>. В процессе работы алгоритма поддерживается инвариант <tex>\rho(u, v) \leqslant d_{uv} \leqslant d_{uv}^{(i)}</tex>, а, поскольку, после выполнения работы алгоритма <tex> \rho(u, v) = d_{uv}^{(i)} </tex>, то тогда будет выполняться и <tex> \rho(u, v) = d_{uv} </tex>. |
{{Утверждение | {{Утверждение | ||
|statement= | |statement= | ||
| − | В течение работы алгоритма Флойда выполняются неравенства: <tex>\rho(u, v) \ | + | В течение работы алгоритма Флойда выполняются неравенства: <tex>\rho(u, v) \leqslant d_{uv} \leqslant d_{uv}^{(i)}</tex>. |
|proof= | |proof= | ||
| Строка 43: | Строка 41: | ||
Пусть также <tex>d'_{uv}</tex> {{---}} значение <tex>d_{uv}</tex> сразу после <tex>i - 1</tex> итерации. | Пусть также <tex>d'_{uv}</tex> {{---}} значение <tex>d_{uv}</tex> сразу после <tex>i - 1</tex> итерации. | ||
| − | Покажем, что <tex> d_{uv} \ | + | Покажем, что <tex> d_{uv} \leqslant d_{uv}^{(i)} </tex>, зная, что <tex> d'_{uv} \leqslant d_{uv}^{(i - 1)} </tex>. |
Рассмотрим два случая: | Рассмотрим два случая: | ||
| − | * Значение <tex> d_{uv}^{(i)} </tex> стало меньше, чем <tex> d_{uv}^{(i - 1)} </tex>. Тогда <tex> d_{uv}^{(i)} = d_{ui}^{(i-1)} + d_{iv}^{(i-1)} \ | + | * Значение <tex> d_{uv}^{(i)} </tex> стало меньше, чем <tex> d_{uv}^{(i - 1)} </tex>. Тогда <tex> d_{uv}^{(i)} = d_{ui}^{(i-1)} + d_{iv}^{(i-1)} \geqslant </tex> (выполняется на шаге <tex> i - 1 </tex>, по индукционному предположению) <tex> \geqslant d'_{ui} + d'_{iv} \ge</tex> (в силу выполнения 7-ой строчки алгоритма на <tex>i</tex>-ой итерации и невозрастания элементов массива <tex> d </tex>) <tex>\geqslant d_{uv}</tex>. |
| − | * В ином случае всё очевидно: <tex> d_{uv}^{(i)} = d_{uv}^{(i - 1)} \ | + | * В ином случае всё очевидно: <tex> d_{uv}^{(i)} = d_{uv}^{(i - 1)} \geqslant d'_{uv} \geqslant d_{uv} </tex>, и неравенство тривиально. |
'''Докажем первое неравенство от противного.''' | '''Докажем первое неравенство от противного.''' | ||
| − | Пусть неравенство было нарушено, рассмотрим момент, когда оно было нарушено впервые. Пусть это была <tex>i</tex>-ая итерация и в этот момент изменилось значение <tex>d_{uv}</tex> и выполнилось <tex>\rho(u,v) > d_{uv}</tex>. Так как <tex>d_{uv}</tex> изменилось, то <tex>d_{uv} = d_{ui} + d_{iv} \ge</tex> (так как ранее <tex>\forall u, v \in V: \rho(u,v) \ | + | Пусть неравенство было нарушено, рассмотрим момент, когда оно было нарушено впервые. Пусть это была <tex>i</tex>-ая итерация и в этот момент изменилось значение <tex>d_{uv}</tex> и выполнилось <tex>\rho(u,v) > d_{uv}</tex>. Так как <tex>d_{uv}</tex> изменилось, то <tex>d_{uv} = d_{ui} + d_{iv} \ge</tex> (так как ранее <tex>\forall u, v \in V: \rho(u,v) \leqslant d_{uv}</tex>) <tex>\geqslant \rho(u, i) + \rho(i, v) \ge</tex> (по неравенству треугольника) <tex>\geqslant \rho(u, v)</tex>. |
| − | Итак <tex>d_{uv} \ | + | Итак <tex>d_{uv} \geqslant \rho(u,v)</tex> {{---}} противоречие. |
}} | }} | ||
| − | + | '''func''' floyd(w)''':''' | |
| − | + | d = w | |
| − | + | '''for''' i = 1 '''to''' n | |
| − | + | '''for''' u = 1 '''to''' n | |
| − | + | '''for''' v = 1 '''to''' n | |
| − | + | d[u][v] = min(d[u][v], d[u][i] + d[i][v]) | |
| − | |||
Данная реализация работает за время <tex> \Theta(n^3) </tex>, но требует уже <tex> \Theta(n^2) </tex> памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении <tex> \Theta </tex> весьма мала. | Данная реализация работает за время <tex> \Theta(n^3) </tex>, но требует уже <tex> \Theta(n^2) </tex> памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении <tex> \Theta </tex> весьма мала. | ||
| Строка 105: | Строка 102: | ||
== Вывод кратчайшего пути == | == Вывод кратчайшего пути == | ||
| − | Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив <tex> | + | Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив <tex>next</tex>, в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из <tex>u</tex> в <tex>v</tex> по кратчайшему пути. |
=== Модифицированный алгоритм === | === Модифицированный алгоритм === | ||
| − | + | '''func''' floyd(w)''':''' | |
| − | + | d = w | |
| − | + | '''for''' i = 1 '''to''' n | |
| − | + | '''for''' u = 1 '''to''' n | |
| − | + | '''for''' v = 1 '''to''' n | |
| − | + | '''if''' d[u][i] + d[i][v] < d[u][v] | |
| − | + | d[u][v] = d[u][i] + d[i][v] | |
| − | + | next[u][v] = i | |
| − | |||
| − | |||
| − | |||
| − | + | '''func''' get_shortest_path(u, v)''':''' | |
| − | + | '''if''' d[u][v] == <tex>\infty</tex> | |
| − | + | '''print''' "No path found" <font color="green">// между вершинами u и v нет пути</font> | |
| − | + | c = u | |
| − | + | '''while''' c != v | |
| − | + | '''print''' c | |
| − | + | c = next[c][v] | |
| − | + | '''print''' v | |
| − | |||
== Нахождение отрицательного цикла == | == Нахождение отрицательного цикла == | ||
| Строка 139: | Строка 132: | ||
Из доказательства следует, что для поиска цикла отрицательного веса необходимо, после завершения работы алгоритма, найти вершину <tex> i </tex>, для которой <tex> d[i][i] < 0 </tex>, и вывести кратчайший путь между парой вершин <tex> (i, i) </tex>. При этом стоит учитывать, что при наличии отрицательного цикла расстояния могут уменьшаться экспоненциально. Для предотвращения переполнения все вычисления стоит ограничивать снизу величиной <tex>-INF</tex>, либо проверять наличие отрицательных чисел на главной диагонали во время подсчета. | Из доказательства следует, что для поиска цикла отрицательного веса необходимо, после завершения работы алгоритма, найти вершину <tex> i </tex>, для которой <tex> d[i][i] < 0 </tex>, и вывести кратчайший путь между парой вершин <tex> (i, i) </tex>. При этом стоит учитывать, что при наличии отрицательного цикла расстояния могут уменьшаться экспоненциально. Для предотвращения переполнения все вычисления стоит ограничивать снизу величиной <tex>-INF</tex>, либо проверять наличие отрицательных чисел на главной диагонали во время подсчета. | ||
== Литература == | == Литература == | ||
| − | * | + | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд — М.: Издательский дом «Вильямс», 2009. — ISBN 978-5-8459-0857-5. |
| + | * [https://ru.wikipedia.org/wiki/Алгоритм_Флойда_—_Уоршелла Википедия - Алгоритм Флойда — Уоршелла] | ||
| + | * [https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm Wikipedia - Floyd–Warshall algorithm] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Кратчайшие пути в графах ]] | [[Категория: Кратчайшие пути в графах ]] | ||
Версия 19:47, 19 декабря 2015
Алгоритм Флойда (алгоритм Флойда–Уоршелла) — алгоритм нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а в случае, когда такой цикл есть, позволяет найти хотя бы один такой цикл. Алгоритм работает за времени и использует памяти. Разработан в 1962 году.
Содержание
Алгоритм
Постановка задачи
Дан взвешенный ориентированный граф ; , в котором вершины пронумерованы от до . Требуется найти матрицу кратчайших расстояний , в которой элемент либо равен длине кратчайшего пути из в , либо равен , если вершина не достижима из .
Описание
Обозначим длину кратчайшего пути между вершинами и , содержащего, помимо и , только вершины из множества как , .
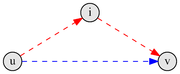
На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер — ) и для всех пар вершин и вычислять . То есть, если кратчайший путь из в , содержащий только вершины из множества , проходит через вершину , то кратчайшим путем из в является кратчайший путь из в , объединенный с кратчайшим путем из в . В противном случае, когда этот путь не содержит вершины , кратчайший путь из в , содержащий только вершины из множества является кратчайшим путем из в , содержащим только вершины из множества .
Код (в первом приближении)
for i = 1 to n for u = 1 to n for v = 1 to n
В итоге получаем, что матрица и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества , что есть попросту все вершины графа. Такая реализация работает за времени и использует памяти.
Код (окончательный)
Утверждается, что можно избавиться от одной размерности в массиве , т.е. использовать двумерный массив . В процессе работы алгоритма поддерживается инвариант , а, поскольку, после выполнения работы алгоритма , то тогда будет выполняться и .
| Утверждение: |
В течение работы алгоритма Флойда выполняются неравенства: . |
|
После инициализации все неравенства, очевидно, выполняются. Далее, массив может измениться только в строчке 5. Докажем второе неравенство индукцией по итерациям алгоритма. Пусть также — значение сразу после итерации. Покажем, что , зная, что . Рассмотрим два случая:
Пусть неравенство было нарушено, рассмотрим момент, когда оно было нарушено впервые. Пусть это была -ая итерация и в этот момент изменилось значение и выполнилось . Так как изменилось, то (так как ранее ) (по неравенству треугольника) . Итак — противоречие. |
func floyd(w):
d = w
for i = 1 to n
for u = 1 to n
for v = 1 to n
d[u][v] = min(d[u][v], d[u][i] + d[i][v])
Данная реализация работает за время , но требует уже памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении весьма мала.
Пример работы
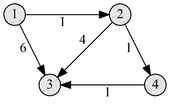 |
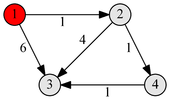 |
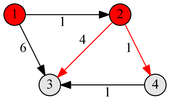 |
 |
|
Вывод кратчайшего пути
Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив , в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из в по кратчайшему пути.
Модифицированный алгоритм
func floyd(w):
d = w
for i = 1 to n
for u = 1 to n
for v = 1 to n
if d[u][i] + d[i][v] < d[u][v]
d[u][v] = d[u][i] + d[i][v]
next[u][v] = i
func get_shortest_path(u, v):
if d[u][v] ==
print "No path found" // между вершинами u и v нет пути
c = u
while c != v
print c
c = next[c][v]
print v
Нахождение отрицательного цикла
| Утверждение: |
При наличии цикла отрицательного веса в матрице появятся отрицательные числа на главной диагонали. |
| Так как алгоритм Флойда последовательно релаксирует расстояния между всеми парами вершин , в том числе и теми, у которых , а начальное расстояние между парой вершин равно нулю, то релаксация может произойти только при наличии вершины такой, что , что эквивалентно наличию отрицательного цикла, проходящего через вершину . |
Из доказательства следует, что для поиска цикла отрицательного веса необходимо, после завершения работы алгоритма, найти вершину , для которой , и вывести кратчайший путь между парой вершин . При этом стоит учитывать, что при наличии отрицательного цикла расстояния могут уменьшаться экспоненциально. Для предотвращения переполнения все вычисления стоит ограничивать снизу величиной , либо проверять наличие отрицательных чисел на главной диагонали во время подсчета.
Литература
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд — М.: Издательский дом «Вильямс», 2009. — ISBN 978-5-8459-0857-5.
- Википедия - Алгоритм Флойда — Уоршелла
- Wikipedia - Floyd–Warshall algorithm