Теорема Татта о существовании полного паросочетания — различия между версиями
Maryann (обсуждение | вклад) м (→Теорема Татта) |
Lytr777 (обсуждение | вклад) м (правки) |
||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition =<tex>odd( | + | |definition =<tex>odd({G})</tex> {{---}} число нечетных компонент связности в графе <tex>{G}</tex>, где '''нечетная компонента''' (англ. ''odd component'') {{---}} это [[Отношение связности, компоненты связности#def2|компонента связности]], содержащая нечетное число вершин. |
}} | }} | ||
{{Определение | {{Определение | ||
| − | |definition ='''Множество Татта''' графа <tex> | + | |definition ='''Множество Татта''' графа <tex>{G}</tex> {{---}} множество <tex>S \subset {V_{G}}</tex>, для которого выполнено условие: <tex>odd({G} \setminus S) > \left\vert S \right\vert</tex> |
}} | }} | ||
==Критерий Татта== | ==Критерий Татта== | ||
| − | Пусть <tex> | + | Пусть <tex>{G'}</tex> {{---}} граф, полученный из <tex>{G}=\langle {V},{E} \rangle</tex> добавлением ребер, при этом в <tex>{G'}</tex> нет [[Теорема Холла#def1|полного паросочетания]], но оно появляется при добавлении любого нового ребра. |
| − | Так как новых вершин не добавлялось, то <tex> | + | Так как новых вершин не добавлялось, то <tex>{G'}=\langle {V},{E'}\rangle </tex> |
| − | Пусть <tex> U = \{ v \in | + | Пусть <tex> U = \{ v \in {V}: deg_{G'} (v) = n - 1 \}</tex>. |
| − | Очевидно, что <tex>\left\vert U \right\vert \ne n</tex>, потому что <tex> | + | Очевидно, что <tex>\left\vert U \right\vert \ne n</tex>, потому что <tex>{G'}</tex> {{---}} не полный граф. |
{{Лемма | {{Лемма | ||
| − | |statement= <tex> | + | |statement= <tex>{G'} \setminus U</tex> {{---}} объединение несвязных полных графов. |
| − | |proof=Пусть это не так, тогда существуют вершины <tex>x,y,z \in | + | |proof=Пусть это не так, тогда существуют вершины <tex>x,y,z \in {V} \setminus U</tex>, такие что <tex>xy, yz \in {E'}</tex>, но <tex>xz \notin {E'}</tex>. Так как <tex>y \notin U</tex>, то <tex>\exists t \notin U: yt \notin {E'}</tex>. |
| − | По построению <tex> | + | По построению <tex>{G'}</tex> в графе <tex>{G'}+xz</tex> существует полное паросочетание <tex>M_1</tex>. Аналогично, в графе <tex>{G'}+yt</tex> существует полное паросочетание <tex>M_2</tex>. Так как в <tex>{G'}</tex> нет полного паросочетания, то <tex>xz \in M_1</tex> и <tex>yt \in M_2</tex>. |
Возможны два случая: | Возможны два случая: | ||
| + | # Вершины <tex>x,z</tex> и <tex>y,t</tex> лежат в разных полных подграфах графа <tex>{G'} \setminus U</tex>, обозначим их <tex>H_1</tex> и <tex>H_2</tex>, соответственно. | ||
| + | #: Покроем вершины подграфа <tex>H_1</tex> паросочетанием <tex>M_2</tex>, при этом заметим, что ребро <tex>xz</tex> не входит в это паросочетание. Аналогично покроем паросочетанием <tex>M_1</tex> вершины подрафа <tex>H_2</tex> и ребро <tex>yt</tex> не войдет в это паросочетание. Если остались непокрытые вершины, то покроем их ребрами из любого паросочетания <tex>M_1</tex> или <tex>M_2</tex>. Таким образом, мы получим полное паросочетание в графе <tex>{G'}</tex>, что противоречит его построению. | ||
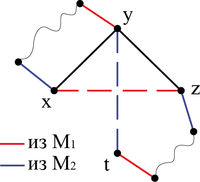
| + | #: [[Файл:Граф_для_теоремы_Татта.png|right|200px|thumb|К доказательству 2-ого пункта леммы.]] | ||
| + | # Вершины <tex>x,y,z</tex> и <tex>t</tex> лежат в одном подграфе графа <tex>{G'} \setminus U</tex>. | ||
| + | #: Построим граф <tex>H</tex>, такой что <tex>{V_{H}}={V}</tex> и <tex>{E_{H}}=M_1 \oplus M_2</tex>. Получим, что вершины <tex>x,y,z</tex> и <tex>t</tex> лежат на каком-то чередующемся цикле из ребер <tex>M_1</tex> и <tex>M_2</tex>. Рассмотрим подробнее, почему это будет именно так. Ребро <tex>xz</tex> принадлежит паросочетанию <tex>M_1</tex>, значит вершина <tex>y</tex> и какая-то произвольная вершина <tex>v</tex> будут покрыты ребром паросочетания <tex>M_1</tex>, при этом эти ребра не принадлежат паросочетанию <tex>M_2</tex>, но ребра <tex>yt</tex> и <tex>vu</tex>, где <tex>u</tex> {{---}} произвольная вершина, принадлежат <tex>M_2</tex> и не принадлежат <tex>M_1</tex> и так далее. Таким образом и получается чередующийся цикл в графе <tex>H</tex>. В силу симметричности <tex>x</tex> и <tex>z</tex> можно считать, что вершины расположены в порядке <tex>tzxy</tex>. Тогда существует путь <tex>P_1=t..zx..y</tex> и полное паросочетание в нем, следовательно существует и путь <tex>P_2=t..zy..x</tex>, содержащий только ребра графа <tex>{G'}</tex>. Тогда на пути <tex>x..y</tex> возьмем ребра из паросочетания <tex>M_2</tex>, а на пути <tex>t..z</tex> - ребра из паросочетания <tex>M_1</tex>. Непокрытыми остались вершины <tex>z</tex> и <tex>y</tex>, которые мы покроем ребром <tex>yz</tex>. Вершины, не принадлежащие рассматриваемому циклу, покроем ребрами любого из паросочетаний <tex>M_1, M_2</tex> (выберем ребра одного из них). Таким образом, получили полное паросочетание в графе <tex>{G'}</tex>, противоречие. | ||
| − | + | В каждом из возможных случаев получили противоречие, значит, наше начальное предположение тоже неверно и <tex>{G'} \setminus U</tex> {{---}} объединение несвязных полных графов, лемма доказана. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | В каждом из возможных случаев получили противоречие, значит, наше начальное предположение тоже неверно и <tex> | ||
}} | }} | ||
| Строка 37: | Строка 34: | ||
{{Теорема | {{Теорема | ||
| − | |statement=В графе <tex> | + | |statement=В графе <tex>{G}</tex> существует полное паросочетание <tex>\Leftrightarrow</tex> <br> |
| − | (то есть в графе <tex> | + | <tex>\forall S \subset {V}</tex> выполнено условие: <tex>odd({G} \setminus S) \leqslant \left\vert S \right\vert</tex> (то есть в графе <tex>{G}</tex> нет ни одного множества Татта) |
|proof = | |proof = | ||
| − | <tex>\Rightarrow</tex> Рассмотрим <tex>M</tex> {{---}} полное паросочетание в графе <tex> | + | <tex>\Rightarrow</tex> <br> |
| + | Рассмотрим <tex>M</tex> {{---}} полное паросочетание в графе <tex>{G}</tex> и множество вершин <tex>S \subset {V}</tex>. | ||
| − | Одна из вершин каждой нечетной компоненты связности графа <tex> | + | Одна из вершин каждой нечетной компоненты связности графа <tex> {G} \setminus S</tex> соединена ребром паросочетания <tex>M</tex> с какой-то вершиной из <tex>S</tex>. Иначе мы не сможем покрыть паросочетанием все вершины этой компоненты связности и получим противоречие с тем, что полное паросочетание существует по условию теоремы. Таким образом, получаем, что <tex>odd({G} \setminus S) \leqslant \left\vert S \right\vert</tex>. |
| − | <tex>\Leftarrow</tex> Пусть для графа <tex> | + | <tex>\Leftarrow</tex> <br> |
| + | Пусть для графа <tex>{G}</tex> выполнено, что <tex>odd({G} \setminus S) \leqslant \left\vert S \right\vert</tex>, но полного паросочетания в этом графе не существует. | ||
| − | Рассмотрим граф <tex> | + | Рассмотрим граф <tex>{G'}</tex> и множество вершин <tex>U</tex> (из леммы). Так как число нечетных компонент не увеличивается при добавлении новых ребер, то <tex>\forall S \subset {V}</tex> выполнено <tex>odd({G'} \setminus S) \leqslant odd({G} \setminus S) \leqslant \left\vert S \right\vert</tex>. По лемме, доказанной выше: <tex>{G'} \setminus U</tex> {{---}} объединение несвязных полных графов. |
| − | Очевидно, что в каждой четной компоненте связности графа <tex> | + | Очевидно, что в каждой четной компоненте связности графа <tex>{G'} \setminus U</tex> мы можем построить полное паросочетание. В каждой нечетной компоненте этого графа построим паросочетание, которое покрывает все вершины кроме одной, оставшуюся непокрытой вершину, соединим с какой-то вершиной множества <tex>U</tex>. При этом мы будем использовать различные вершины из <tex>U</tex>, это возможно, так как <tex>odd({G'} \setminus U) \leqslant \left\vert U \right\vert</tex>. Если все вершины множества <tex>U</tex> оказались покрытыми, то мы получили полное паросочетание в графе <tex>{G'}</tex>. Противоречие, так как по построению в <tex>{G'}</tex> нет полного паросочетания. |
| − | Значит, в <tex>U</tex> осталось какое-то количество непокрытых вершин, при этом их четное число, потому что число вершин в <tex> | + | Значит, в <tex>U</tex> осталось какое-то количество непокрытых вершин, при этом их четное число, потому что число вершин в <tex>{G'}</tex> четно, так как <tex>odd({G'} \setminus \varnothing) \leqslant \left\vert \varnothing \right\vert = 0</tex> и уже покрыто паросочетанием четное число вершин. Так как в множество <tex>U</tex> входят вершины, которые в <tex>{G'}</tex> смежны со всеми остальными, то мы сможем разбить оставшиеся вершины на пары и покрыть их паросочетанием. |
| − | Таким образом, получили в <tex> | + | Таким образом, получили в <tex>{G'}</tex> полное паросочетание, что противоречит тому, как мы задали этот граф изначально. Значит, начальное предположение не верно, и в <tex>{G}</tex> существует полное паросочетание. |
| − | |||
| − | Значит, начальное предположение не верно, и в <tex> | ||
}} | }} | ||
| − | == | + | == Примечание == |
| + | *[http://ru.wikipedia.org/wiki/%D1%E8%EC%EC%E5%F2%F0%E8%F7%E5%F1%EA%E0%FF_%F0%E0%E7%ED%EE%F1%F2%FC Симметрическая разность] | ||
| + | |||
| + | == Источники информации == | ||
*[http://logic.pdmi.ras.ru/~dvk/211/graphs_dk.pdf Д.В Карпов. Теория графов] (2 глава, стр. 29) | *[http://logic.pdmi.ras.ru/~dvk/211/graphs_dk.pdf Д.В Карпов. Теория графов] (2 глава, стр. 29) | ||
| − | * [http://en.wikipedia.org/wiki/Tutte_theorem Wikipedia — Tutte theorem] | + | *[http://en.wikipedia.org/wiki/Tutte_theorem Wikipedia — Tutte theorem] |
[[Категория:Алгоритмы и структуры данных]] | [[Категория:Алгоритмы и структуры данных]] | ||
[[Категория:Задача о паросочетании]] | [[Категория:Задача о паросочетании]] | ||
Версия 10:42, 14 января 2016
| Определение: |
| — число нечетных компонент связности в графе , где нечетная компонента (англ. odd component) — это компонента связности, содержащая нечетное число вершин. |
| Определение: |
| Множество Татта графа — множество , для которого выполнено условие: |
Критерий Татта
Пусть — граф, полученный из добавлением ребер, при этом в нет полного паросочетания, но оно появляется при добавлении любого нового ребра.
Так как новых вершин не добавлялось, то
Пусть .
Очевидно, что , потому что — не полный граф.
| Лемма: |
— объединение несвязных полных графов. |
| Доказательство: |
|
Пусть это не так, тогда существуют вершины , такие что , но . Так как , то . По построению в графе существует полное паросочетание . Аналогично, в графе существует полное паросочетание . Так как в нет полного паросочетания, то и . Возможны два случая:
|
Теорема Татта
| Теорема: |
В графе существует полное паросочетание выполнено условие: (то есть в графе нет ни одного множества Татта) |
| Доказательство: |
|
Одна из вершин каждой нечетной компоненты связности графа соединена ребром паросочетания с какой-то вершиной из . Иначе мы не сможем покрыть паросочетанием все вершины этой компоненты связности и получим противоречие с тем, что полное паросочетание существует по условию теоремы. Таким образом, получаем, что . Рассмотрим граф и множество вершин (из леммы). Так как число нечетных компонент не увеличивается при добавлении новых ребер, то выполнено . По лемме, доказанной выше: — объединение несвязных полных графов. Очевидно, что в каждой четной компоненте связности графа мы можем построить полное паросочетание. В каждой нечетной компоненте этого графа построим паросочетание, которое покрывает все вершины кроме одной, оставшуюся непокрытой вершину, соединим с какой-то вершиной множества . При этом мы будем использовать различные вершины из , это возможно, так как . Если все вершины множества оказались покрытыми, то мы получили полное паросочетание в графе . Противоречие, так как по построению в нет полного паросочетания. Значит, в осталось какое-то количество непокрытых вершин, при этом их четное число, потому что число вершин в четно, так как и уже покрыто паросочетанием четное число вершин. Так как в множество входят вершины, которые в смежны со всеми остальными, то мы сможем разбить оставшиеся вершины на пары и покрыть их паросочетанием. Таким образом, получили в полное паросочетание, что противоречит тому, как мы задали этот граф изначально. Значит, начальное предположение не верно, и в существует полное паросочетание. |
Примечание
Источники информации
- Д.В Карпов. Теория графов (2 глава, стр. 29)
- Wikipedia — Tutte theorem