Поиск в матрице — различия между версиями
Kolchanov (обсуждение | вклад) (→Решение за O(n\cdotlog(m))) |
Kolchanov (обсуждение | вклад) (→Код) |
||
| Строка 33: | Строка 33: | ||
'''if''' (target < a[0][0] || target > a[N-1][N-1]) | '''if''' (target < a[0][0] || target > a[N-1][N-1]) | ||
| − | '''return''' false | + | '''return''' false |
| − | row = 0 | + | row = 0 |
| − | col = N-1 | + | col = N-1 |
| − | '''while''' (row <= N-1 && col >= 0) | + | '''while''' (row <= N-1 && col >= 0) |
'''if''' (a[row][col] < target) | '''if''' (a[row][col] < target) | ||
| − | row++ | + | row++ |
'''else if''' (a[row][col] > target) | '''else if''' (a[row][col] > target) | ||
| − | col-- | + | col-- |
'''else''' | '''else''' | ||
| − | '''return''' true | + | '''return''' true |
| − | '''return''' false | + | '''return''' false |
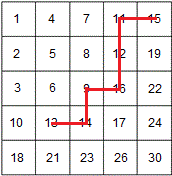
[[Файл:find13.png|320px|thumb|right|Пример поиска числа 13 в матрице]] | [[Файл:find13.png|320px|thumb|right|Пример поиска числа 13 в матрице]] | ||
Версия 15:34, 23 января 2016
| Задача: |
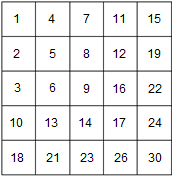
| Задана отсортированная двумерная матрица, состоящая из n строк и m столбцов. Необходимо найти расположение указанного элемента в матрице или определить, что данный элемент в матрице отсутствует. |
| Определение: |
| Отсортированная матрица - матрица, для которой выполнено следующее условие: |
Содержание
Решение за O(nm)
Для начала рассмотрим наивный алгоритм поиска элемента. В каждой строке исходной матрицы запускаем линейный поиск, если находим элемент, то возвращаем его координаты . Время работы — .
Решение за O(nlog(m))
Данный способ решения использует наивное решение за , улучшенное с помощью двоичного поиска. Для этого в каждой строке запускается двоичный поиск. Время работы — .
Замечание
Время работы может быть улучшено до . Для этого необходимо модифицировать алгоритм так, чтобы в том случае, если столбцов больше чем строк, он бы запускал двоичный поиск по строкам, если строк больше — наоборот.
Существует еще один способ оптимизации. Рассмотрим случай, когда используется двоичный поиск по строке. Достаточно очевидно, что искомое число может находится только в тех строках, где первый элемент меньше искомого, а последний - больше. Перед началом поиска можно исключить 2 прямоугольных участка матрицы: первый состоит из строк, у которых последний элемент меньше искомого; второй состоит из строк, у которых первый элемент больше искомого. Используя двоичный поиск, можно найти границы этих участков за для столбцов и за строк.
Решение за O(n + m)
В данном решении мы начинаем поиск из правого верхнего угла и движемся к искомому элементу. Идея алгоритма в том, что если текущий элемент меньше необходимого, то мы сдвигаемся на одну строку вниз. Если он больше, то мы сдвигаемся на одну колонку вправо.
Код
if (target < a[0][0] || target > a[N-1][N-1])
return false
row = 0
col = N-1
while (row <= N-1 && col >= 0)
if (a[row][col] < target)
row++
else if (a[row][col] > target)
col--
else
return true
return false
Оценка времени работы
Очевидно, что во время работы указатель сдвигается максимум на n строк и m столбцов. В этом случае время работы составляет .