Двудольные графы и раскраска в 2 цвета — различия между версиями
(→Теорема Кенига) |
Kozlov ea (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | + | == Двудольный граф == | |
| − | + | ||
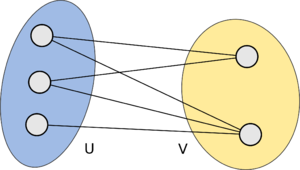
| − | + | [[Файл: Bipartite_graph.png|300px|thumb|center|Пример [[Основные_определения_теории_графов#Двудольный_граф |двудольного]] графа]] | |
| − | |||
| − | |||
| − | [[Файл: Bipartite_graph.png|thumb| | ||
== Раскраска в 2 цвета == | == Раскраска в 2 цвета == | ||
| Строка 10: | Строка 7: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Граф 2-раскрашиваемый тогда и только тогда, когда он двудольный. | + | Граф 2-раскрашиваемый тогда и только тогда, когда он двудольный (англ. '' bipartite graph'' or ''bigraph''). |
|proof= | |proof= | ||
Если множество вершин двудольного графа можно разделить на два независимых подмножества так, что ни одна из вершин ни в одном из этих подмножеств не является смежной к вершине из этого же подмножества, тогда граф <tex>G = (W, E)</tex> — 2-раскрашиваем. <tex>\chi(G) = 2</tex>. | Если множество вершин двудольного графа можно разделить на два независимых подмножества так, что ни одна из вершин ни в одном из этих подмножеств не является смежной к вершине из этого же подмножества, тогда граф <tex>G = (W, E)</tex> — 2-раскрашиваем. <tex>\chi(G) = 2</tex>. | ||
| Строка 17: | Строка 14: | ||
}} | }} | ||
| − | ==Теорема | + | ==Теорема Кёнига== |
{{Теорема | {{Теорема | ||
|about= | |about= | ||
| − | + | Кёниг | |
|statement= | |statement= | ||
Граф <tex> G </tex> является двудольным тогда и только тогда, когда все циклы в графе <tex> G </tex> имеют чётную длину. | Граф <tex> G </tex> является двудольным тогда и только тогда, когда все циклы в графе <tex> G </tex> имеют чётную длину. | ||
| Строка 36: | Строка 33: | ||
}} | }} | ||
| − | == Алгоритм == | + | == Следствие == |
| + | |||
| + | ===Алгоритм проверки графа на двудольность, используя обход в глубину=== | ||
| − | Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину. | + | Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину (англ. ''Depth-first search''). |
| − | На каждом шаге обхода в глубину помечаем вершину. Допустим мы пошли в первую вершину — помечаем её как <tex> 1 </tex>. Затем просматриваем все смежные вершины и если не помечена вершина, то на ней ставим пометку <tex> 2 </tex> и рекурсивно переходим в нее. Если же она помечена и на ней стоит та же пометка, что и у той, из которой шли (в нашем случае <tex> 1 </tex>), значит граф не двудольный. | + | На каждом шаге обхода в глубину помечаем вершину. Допустим, мы пошли в первую вершину — помечаем её как <tex> 1 </tex>. Затем просматриваем все смежные вершины, и если не помечена вершина, то на ней ставим пометку <tex> 2 </tex> и рекурсивно переходим в нее. Если же она помечена и на ней стоит та же пометка, что и у той, из которой шли (в нашем случае <tex> 1 </tex>), значит граф не двудольный. |
| + | ===Алгоритм проверки графа на двудольность, используя обход в ширину=== | ||
| − | + | Произведём серию поисков в ширину (англ. ''Breadth-first search''). Т.е. будем запускать поиск в ширину из каждой непосещённой вершины. Ту вершину, из которой мы начинаем идти, мы помещаем в первую долю. В процессе поиска в ширину, если мы идём в какую-то новую вершину, то мы помещаем её в долю, отличную от доли текущей вершину. Если же мы пытаемся пройти по ребру в вершину, которая уже посещена, то мы проверяем, чтобы эта вершина и текущая вершина находились в разных долях. В противном случае граф двудольным не является. | |
| − | + | По окончании работы алгоритма мы либо обнаружим, что граф не двудолен, либо найдём разбиение вершин графа на две доли. | |
| − | |||
==См. также == | ==См. также == | ||
* [http://rain.ifmo.ru/cat/view.php/theory/graph-coloring-layout| Графы. Раскраски и укладки.] | * [http://rain.ifmo.ru/cat/view.php/theory/graph-coloring-layout| Графы. Раскраски и укладки.] | ||
| + | |||
| + | == Источники == | ||
| + | * Асанов М. О., Баранский В. А., Расин В. В. - Дискретная математика: Графы, матроиды, алгоритмы. | ||
| + | * Харари Ф. - Теория графов. | ||
| + | * [http://en.wikipedia.org/wiki/K%C3%B6nig's_theorem_(graph_theory) Теорема Кёнига] | ||
| + | * [http://e-maxx.ru/algo/bipartite_checking MAXimal :: algo :: Проверка графа на двудольность] | ||
| + | * [http://www.e-maxx.ru/algo/dfs Обход в глубину. Реализации.] | ||
| + | * [http://e-maxx.ru/algo/bfs Обход в ширину. Реализации.] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Раскраски графов]] | [[Категория: Раскраски графов]] | ||
Версия 02:15, 26 января 2016
Содержание
Двудольный граф
Раскраска в 2 цвета
| Теорема: |
Граф 2-раскрашиваемый тогда и только тогда, когда он двудольный (англ. bipartite graph or bigraph). |
| Доказательство: |
|
Если множество вершин двудольного графа можно разделить на два независимых подмножества так, что ни одна из вершин ни в одном из этих подмножеств не является смежной к вершине из этого же подмножества, тогда граф — 2-раскрашиваем. . Если же граф 2-раскрашиваемый, то множество его вершин можно разделить на два непересекающихся множества так, чтобы в каждом из них не нашлось двух смежных вершин. Тогда граф будет двудольным. |
Теорема Кёнига
| Теорема (Кёниг): |
Граф является двудольным тогда и только тогда, когда все циклы в графе имеют чётную длину. |
| Доказательство: |
|
Достаточность. Рассмотрим двудольный граф. Начнем цикл в доле . Нужно пройти по четному числу ребер, чтобы вернуться в снова. Следовательно, при замыкании цикла число ребер будет четным. Необходимость. Пусть ненулевой граф связен и не имеет циклов нечетной длины. Выберем произвольно вершину и разобьем множество всех вершин на два непересекающихся множества и так, чтобы в лежали вершины , такие что кратчайшая цепь была чётной длины, а в соответственно вершины , для которых длина цепи — нечётная. При этом . В графе нет ребер , таких что лежат одновременно в и . Докажем это от противного. Пусть . Зададим — кратчайшая цепь, а — кратчайшая цепь. Обе цепи четной длины. Пусть — последняя вершина цепи , принадлежащая . Тогда подцепи от до в и имеют одинаковую длину (иначе бы, пройдя по более короткой подцепи от до мы смогли бы найти более короткую цепь от до или от до , чем цепь или ). Так как подцепи от до и от до в цепях и имеют одинаковую четность, а значит в сумме с ребром они образуют цикл нечётной длины, что невозможно. |
Следствие
Алгоритм проверки графа на двудольность, используя обход в глубину
Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину (англ. Depth-first search). На каждом шаге обхода в глубину помечаем вершину. Допустим, мы пошли в первую вершину — помечаем её как . Затем просматриваем все смежные вершины, и если не помечена вершина, то на ней ставим пометку и рекурсивно переходим в нее. Если же она помечена и на ней стоит та же пометка, что и у той, из которой шли (в нашем случае ), значит граф не двудольный.
Алгоритм проверки графа на двудольность, используя обход в ширину
Произведём серию поисков в ширину (англ. Breadth-first search). Т.е. будем запускать поиск в ширину из каждой непосещённой вершины. Ту вершину, из которой мы начинаем идти, мы помещаем в первую долю. В процессе поиска в ширину, если мы идём в какую-то новую вершину, то мы помещаем её в долю, отличную от доли текущей вершину. Если же мы пытаемся пройти по ребру в вершину, которая уже посещена, то мы проверяем, чтобы эта вершина и текущая вершина находились в разных долях. В противном случае граф двудольным не является. По окончании работы алгоритма мы либо обнаружим, что граф не двудолен, либо найдём разбиение вершин графа на две доли.
См. также
Источники
- Асанов М. О., Баранский В. А., Расин В. В. - Дискретная математика: Графы, матроиды, алгоритмы.
- Харари Ф. - Теория графов.
- Теорема Кёнига
- MAXimal :: algo :: Проверка графа на двудольность
- Обход в глубину. Реализации.
- Обход в ширину. Реализации.