Формула включения-исключения — различия между версиями
(→Формула включения-исключения) |
|||
| Строка 13: | Строка 13: | ||
{{Теорема | {{Теорема | ||
| − | |statement=Пусть <tex> A = \ | + | |statement=Пусть <tex> A = \bigcup \limits_{i=1}^{n}A_i </tex> , тогда по формуле включения-исключения: <center> <tex> | A | = \sum \limits_{I=(i_1,i_2, \ldots ,i_k) \subset \{ 1,2, \ldots ,n \} } (-1)^{k+1} \Big| \bigcap \limits_{ j \in I } A_j \Big| </tex> </center> |
||proof=Для случая <tex>~n=1</tex> и <tex>~n=2</tex> теорема, очевидно, верна. | ||proof=Для случая <tex>~n=1</tex> и <tex>~n=2</tex> теорема, очевидно, верна. | ||
| Строка 19: | Строка 19: | ||
Теперь рассмотрим <tex>~n>2</tex>: | Теперь рассмотрим <tex>~n>2</tex>: | ||
<center> | <center> | ||
| − | <tex> A = \ | + | <tex> A = \bigcup \limits_{i=1}^{n}A_i = \Bigg( \underbrace {\bigcup \limits_{i=1}^{n-1}A_i}_{B} \Bigg) \cup A_n </tex> |
| − | <tex> | B | = \ | + | <tex> | B | = \sum \limits_{I \subset \{ 1,2, \ldots ,n-1 \} } (-1)^{|I|+1} \Big| \bigcap \limits_{ j \in I } A_j \Big| </tex> |
| Строка 28: | Строка 28: | ||
| − | <tex> \Big| B \bigcap A_n \Big| = \Bigg| \Bigg( \ | + | <tex> \Big| B \bigcap A_n \Big| = \Bigg| \Bigg( \bigcup \limits_{i=1}^{n-1}A_i \Bigg) \bigcap A_n \Bigg|= \Bigg| \bigcup \limits_{i=1}^{n-1} \bigg( A_i \bigcap A_n \bigg) \Bigg| = </tex> |
| − | <tex> = \ | + | <tex> = \sum \limits_{I \subset \{ 1,2, \ldots ,n-1 \} } (-1)^{|I|+1} \bigg| \bigcap \limits_{ j \in I } \Big( A_j \bigcap A_n \Big) \bigg| = \sum \limits_{I \subset \{ 1,2, \ldots ,n-1 \} } (-1)^{|I|+1} \Big| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \Big| </tex> |
</center> | </center> | ||
| Строка 41: | Строка 41: | ||
<center> | <center> | ||
| − | <tex> | A | = | A_n| + \Bigg( \ | + | <tex> | A |=| A_n |+\Bigg( \sum \limits_{I \subset \{ 1,2, \ldots ,n-1 \} } (-1)^{|I|+1} \Big| \bigcap \limits_{ j \in I } A_j \Big| \Bigg) - - \Bigg( \sum \limits_{I \subset \{ 1,2, \ldots ,n-1 \} } (-1)^{|I|+1} \Big| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \Big| \Bigg) = \sum \limits_{I \subset \{ 1,2, \ldots ,n \} } (-1)^{|I|+1} \Big| \bigcap \limits_{ j \in I } A_j \Big| </tex> |
</center> | </center> | ||
}} | }} | ||
Версия 19:11, 26 ноября 2010
Формула включения-исключения
Формула включения-исключения - это комбинаторная формула, которая позволяет определить мощность объединения конечных множеств, если известны их мощности и мощности всех их возможных пересечений.
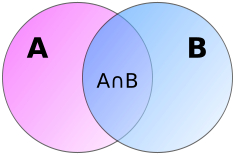
Например, в случае двух множеств формула включения-исключения имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
| Теорема: |
Пусть , тогда по формуле включения-исключения: |
| Доказательство: |
|
Для случая и теорема, очевидно, верна. Теперь рассмотрим :
Таким образом:
|