Техника частичного каскадирования — различия между версиями
(Добавлен первый способ решения) |
(Закончена тема "различные подходы к решению") |
||
| Строка 2: | Строка 2: | ||
{{Задача | {{Задача | ||
| − | |definition = Дано <tex> k </tex> каталогов <tex> C_i </tex>, каталог <tex>i</tex> представляет собой упорядоченный массив размера <tex> n_i </tex>. Поступают запросы, которые представляют собой один элемент <tex> x </tex>. Требуется для каждого запроса определить в каждом каталоге элемент меньше либо равный <tex> x </tex>. | + | |definition = Дано <tex> k </tex> каталогов <tex> C_i </tex>, каталог <tex>i</tex> представляет собой упорядоченный массив размера <tex> n_i </tex>. Поступают запросы, которые представляют собой один элемент <tex> x </tex>. Требуется для каждого запроса определить в каждом каталоге максимальный элемент меньше либо равный <tex> x </tex>. |
}} | }} | ||
| + | |||
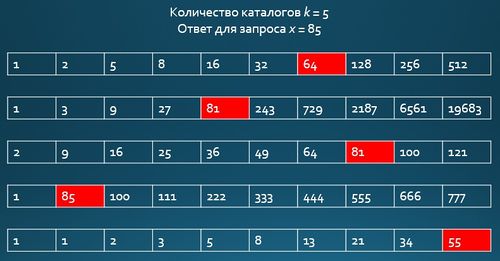
| + | [[Файл:FCT_pic1.jpg|500px|right|thumb|Пример ответа на запрос]] | ||
== Различные подходы к решению == | == Различные подходы к решению == | ||
| Строка 11: | Строка 13: | ||
1) Пусть пришел запрос <tex> x </tex>. Пробежимся по всем каталогам. Пусть мы находимся в <tex> i</tex>-ом каталоге, тогда мы можем ответить на запрос для данного каталога за <tex> O(\log n_i) </tex> используя бинарный поиск. Так как каталогов <tex> k </tex> штук, то в итоге мы обработаем запрос за <tex> O(k \log n) </tex>. Для хранения всех каталогов понадобится <tex> \Theta(n) </tex> памяти. | 1) Пусть пришел запрос <tex> x </tex>. Пробежимся по всем каталогам. Пусть мы находимся в <tex> i</tex>-ом каталоге, тогда мы можем ответить на запрос для данного каталога за <tex> O(\log n_i) </tex> используя бинарный поиск. Так как каталогов <tex> k </tex> штук, то в итоге мы обработаем запрос за <tex> O(k \log n) </tex>. Для хранения всех каталогов понадобится <tex> \Theta(n) </tex> памяти. | ||
<br> | <br> | ||
| + | 2) Для второго способа построим сбалансированное бинарное дерево поиска их всех элементов всех каталогов. В каждой вершине дерева будет хранится дополнительно кортеж из <tex> k </tex> элементов - максимальных представителей каталогов меньше либо равных ключу вершины. Таким образом такая структура будет занимать <tex> O(n) </tex> на дерево поиска и <tex> O(kn) </tex> на дополнительные кортежи.Тогда для ответа на запрос <tex> x </tex> найдем в дереве поиска максимальный ключ меньше либо равный <tex> x </tex> и выведем <tex> k </tex> элементов соответствующего кортежа, итого ответ на запрос производится за <tex> O(\log n + k) </tex>. | ||
| + | <br> <br> | ||
| + | Итого имеем | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Тип подхода к решению !! Необходимая память !! Время ответа на один запрос | ||
| + | |- | ||
| + | | <center><tex> k </tex> бинарных поисков </center> || <center><tex> \Theta(n) </tex></center> || <center><tex> O(k \log n) </tex></center> | ||
| + | |- | ||
| + | | <center>Построение бинарного дерева поиска с кортежами</center> || <center><tex> O(kn) </tex></center> || <center><tex> O(\log n + k) </tex></center> | ||
| + | |} | ||
Версия 16:25, 7 июня 2017
Техника частичного каскадирования (англ. fractional cascading technique) — это способ организации структуры данных, который предназначен для быстрого итеративного поиска в каталогах.
| Задача: |
| Дано каталогов , каталог представляет собой упорядоченный массив размера . Поступают запросы, которые представляют собой один элемент . Требуется для каждого запроса определить в каждом каталоге максимальный элемент меньше либо равный . |
Различные подходы к решению
Пусть .
1) Пусть пришел запрос . Пробежимся по всем каталогам. Пусть мы находимся в -ом каталоге, тогда мы можем ответить на запрос для данного каталога за используя бинарный поиск. Так как каталогов штук, то в итоге мы обработаем запрос за . Для хранения всех каталогов понадобится памяти.
2) Для второго способа построим сбалансированное бинарное дерево поиска их всех элементов всех каталогов. В каждой вершине дерева будет хранится дополнительно кортеж из элементов - максимальных представителей каталогов меньше либо равных ключу вершины. Таким образом такая структура будет занимать на дерево поиска и на дополнительные кортежи.Тогда для ответа на запрос найдем в дереве поиска максимальный ключ меньше либо равный и выведем элементов соответствующего кортежа, итого ответ на запрос производится за .
Итого имеем
| Тип подхода к решению | Необходимая память | Время ответа на один запрос |
|---|---|---|
| |
|
|
| |
|
|