Графы де Брюина

Определение:

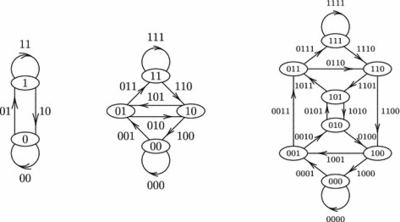
Графом де Брюина (англ. De Bruijn graph) с параметром [math]l[/math] для [math]n[/math]-буквенного алфавита называется ориентированный граф [math]G(V, E)[/math], где [math] V - [/math] множество всех слов длины [math]l[/math] в заданном алфавите, и [math]e = (u, v) \in E \Leftrightarrow \exists [/math] слово [math]L[/math] длины [math]l+1[/math] в заданном алфавите такое, что [math] u = prefix(L) [/math] и [math] v = suffix(L) [/math]. Обозначается как [math] B(n, l) [/math]

Основные свойства

Лемма (об эйлеровости графа):

[math]B(n, l)\ - [/math] эйлеров

Доказательство:

[math]\triangleright[/math]

Ориентированный граф является эйлеровым, если число входящих рёбер равно числу исходящих. Докажем, что это верно для [math] B(n, l) [/math]. А именно, что [math] \forall v \in V [/math] верно, что [math] deg_{out}(v) = n = deg_{in}(v)[/math]. Докажем первое равенство, второе аналогично. Существует ровно [math] n [/math] символов алфавита, которые можно добавить в конец слова [math] \alpha[/math], соответствующему вершине [math] v [/math]. Получим ровно [math] n [/math] различных слов. И у всех этих слов различные суффиксы длины [math] l [/math]. Таким образом, из вершины [math] v [/math] выходит ровно [math] n [/math] рёбер и входит тоже [math] n [/math] рёбер. Значит, граф де Брюина [math] - [/math] эйлеров.

[math]\triangleleft[/math]

Лемма (о количестве вершин и рёбер в графе):

В [math] B(n, l) \ |V| = n^l, |E| = n^{l+1}[/math]

Доказательство:

[math]\triangleright[/math]

Число вершин очевидно находится из определения графа и равно [math] n^l [/math]. Число рёбер следует из доказательства предыдущей леммы: каждой вершине инцидентно ровно [math] 2n [/math] ребер. Таким образом, [math] |E| = \frac{1}{2} \cdot n^l \cdot 2n = n^{l+1} [/math]

[math]\triangleleft[/math]

Лемма (о равносильном определении):

В [math] B(n, l) \ (u, v) \in E \Leftrightarrow [/math] [math] prefix_{l-1}(v) = suffix_{l-1}(u) [/math]

Доказательство:

[math]\triangleright[/math]

[math] \Leftarrow [/math] Составим слово длины [math]l+1 \ L = a \gamma b [/math], тогда [math] \gamma b = suffix(L), a \gamma = prefix(L) [/math] . При этом [math] |a \gamma| = |\gamma b| = |L|-1 = l [/math]. Если выбрать [math] a, b \ [/math] как первый и последний символ слов [math] u, v [/math] соответственно, и взять [math] \gamma = prefix_{l-1}(v) = suffix_{l-1}(u) [/math], то ребро между этими вершинами есть по определению. [math] \Rightarrow [/math] Возьмём подстроку слова [math] L [/math] (из определения) без крайних символов (её длина [math] l - 1 [/math]). Так же из определения следует, что это будет суффиксом строки, соответствующей вершине [math] u [/math], и префиксом для строки, соответствующей [math] v [/math].

[math]\triangleleft[/math]

Лемма (о графе с [math] l = 1 [/math]):

[math] B(n, 1)\ - [/math] полный граф.

Доказательство:

[math]\triangleright[/math]

Действительно, для любых (необязательно различных) вершин [math] u, v \ \exists L = \alpha \beta [/math], где [math] \alpha, \beta - [/math] слова (символы), соответствующие вершинам [math] u, v [/math]. И тогда очевидно, что существует ребро [math] e = (u, v)\ \forall u, v \in V [/math].

[math]\triangleleft[/math]

Алгоритм построения

Задача:

Дан алфавит длины [math] n [/math] и длина слов [math] l [/math]. Построить по ним граф де Брюина.

Алгоритм:

1. Создаём пустой граф из [math] n^l [/math] вершин.

2. Генерируем слово длины [math] l+1 [/math].

3. Считаем префикс [math] pref [/math] и суффикс [math] suff [/math] длины [math] l [/math] для текущего. Причём установим в алфавите отношение порядка и будем рассматривать его символы как цифры в [math] n [/math]-значной системе счисления.

4. Проводим ребро [math] (pref, suff) [/math] в графе. Переходим к пункту [math] 2 [/math] (например, будем перебирать в порядке лексикографического возрастания), пока не будут перебраны все слова длины [math] l+1 [/math].

Корректность: перебраны все слова длины [math] l+1 [/math], следовательно, были рассмотрены все возможные пары вершин, между которыми проведено ребро.

Время работы: [math] O(n^{l+1} \cdot substring) = O(|E| \cdot l) [/math]

Применение графов де Брюина

Задача:

Известно, что пароль имеет длину [math] l [/math], и состоит из цифр от [math] 1 [/math] до [math] n [/math]. Требуется вывести кратчайшую последовательность цифр, которая гарантированно содержит пароль как подстроку.

Построенный граф Де Брюина для двоичного алфавита со словами [math] L [/math] (из определения) на рёбрах

Решение:

1. Составим граф де Брюина [math] (n, l-1) [/math].

2. Найдём в построенном графе эйлеров цикл. Он существует, так как граф де Брюина эйлеров по первой лемме.

3. Слово, соответствующее первой вершине цикла, возьмём полностью ([math] l - 1 [/math] символов), затем будем последовательно добавлять в конец строки последний символ слова вершины, в которую был осуществлён переход. Так как рёбер [math] n^l [/math], получим последовательность длиной [math] n^l + l - 1 [/math].

Корректность:

1. Очевидно, что последовательность меньшей длины составить нельзя: в полученной последовательности ровно [math] n^l [/math] подстрок длины [math] l [/math], и именно столько чисел можно составить из цифр от [math] 1 [/math] до [math] n [/math].

2. Двум разным рёбрам [math] e_1 = (u_1, v_1), e_2 = (u_2, v_2) [/math] соответствует два различных слова [math] L [/math] длины [math] l [/math]. Иначе [math] u_{1} = prefix(L) = u_{2} [/math] и [math] v_{1} = suffix(L) = v_{2} [/math]. То есть это одно и то же ребро, при этом кратных рёбер в графе нет.

3. Отсюда следует, что в последовательности содержится [math] n^l [/math] различных подстрок длины [math] l [/math]. И короче последовательность получить нельзя. Значит, мы получили ответ за [math] O((|E| \cdot (l-1)) + (|E| + |V|)) = O(|E| \cdot (l-1)) [/math], то есть за время построения графа де Брюина [math] (n, l-1) [/math].

Задача:

Даны неповторяющиеся последовательности нуклеотидов (риды) длины [math] l [/math]. Известно, что все подстроки генома длины [math] l [/math] входят в данное множество ридов. Построить возможный геном.

Подграф графа Де Брюина для ридов, указанных на рёбрах. Искомый геном: ACGTACTAT

Пояснение:

Геном (как и его части [math] - [/math] риды) является словом из [math]4[/math]-символьного алфавита [math] \{A, G, C, T\} [/math], где символы так же называются нуклеотидами. В реальности длины ридов находятся обычно в диапазоне [math] 100 [/math]-[math] 1000 [/math] нуклеотидов, а геном может содержать от [math] 10^6 [/math] нуклеотидов у простейших организмов. При этом учёные могут получать информацию только о ридах (в силу размера последовательностей) физическим путем (метод секвенирования).

Решение:

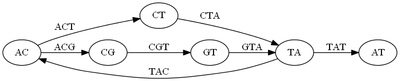
Решение этой задачи очень простое после решения предыдущей задачи. Построим граф [math] G [/math], где вершинами будут являться суффиксы и префиксы длины [math] l - 1 [/math] всех ридов. Получили подграф графа де Брюина [math] (4, l-1) [/math] (подграф, так как в нём есть не обязательно все [math] 4^{l - 1} [/math] вершины), где каждому ребру соответствует рид. Найдём в нём эйлеров путь. Он существует, так как на геном было наложено условие о том, что все его подстроки длины [math] l [/math] входят в наше множество ридов. Этот путь является возможным ответом. Очевидно, что единственно верный ответ (коим является реальный геном реального существа) получить можно не всегда, так как не всегда в графе есть единственный эйлеров путь.

Комментарий:

К сожалению, кроме того, что алгоритм работает за [math] O(4^l \cdot l) [/math], в реальности есть немало технических проблем:

1. Как можно догадаться из пояснения: едва ли риды обязательно будут неповторяющимися.

2. Данные о ридах могут быть получены лишь с некоторой вероятностью (как правило, ошибка в нуклеотиде имеет вероятность около [math] 0.001 [/math], но вблизи "края" генома она может достигать и [math] 0.3 [/math]).

3. Риды не могут иметь фиксированную длину в силу особенностей метода секвенирования.

Вывод:

Несмотря на то, что задача не решается в общем случае приведённым алгоритмом, граф де Брюина действительно используется в ассемблерах (программах, собирающих геном или его большие части из ридов), но с заметными усложнениями.

См. также

• Основные определения, связанные со строками
• Эйлеровость графов
• Алгоритм построения Эйлерова цикла

Источники информации

• Wikipedia — De Bruijn graph
• Нурк Сергей — Разработка алгоритмов обработки графа де Брюина в задаче геномного ассемблирования