Конструирование комбинаторных объектов и их подсчёт

Последовательности(Seq)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{n}\}[/math] — множество из различных объектов, [math]S=Seq(A)[/math] — множество всех последовательностей из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{m}\}[/math] — количество объектов веса [math]\{1 \ldots m\}[/math]. Тогда количество последовательностей веса [math]n[/math] можно вычислить как: [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-i}[/math].

Подсчет битовых векторов длины [math]n[/math]

Пусть [math]A=\{0, 1\}[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]S=Seq(A)[/math] — множество всех битовых векторов.

Тогда, [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-i}=2S_{n-1}=2^{n}[/math].

Подсчет Seq из маленьких и больших элементов

Пусть [math]A=\{1, 2\}[/math], [math]W=\{1, 1, 0 \ldots 0\}[/math], [math]S=Seq(A)[/math] — множество всех последовательностей из маленьких и больших элементов [math]S=Seq(A)[/math].

Тогда, [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-1}=S_{n-1}+S_{n-2}=F_{n}[/math], где [math]F_{n}[/math] — [math]n[/math]-ое число Фибоначчи .

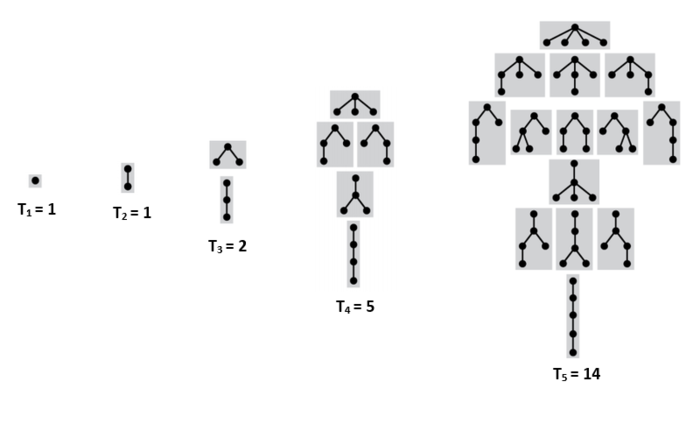
Подсчет подвешенных непомеченных деревьев с порядком на детях

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами, [math]T_{0} = 1[/math]. [math]S=Seq(A)[/math] — множество всех последовательностей из данных деревьев. [math]S_{n}[/math] — количество последовательностей с суммарным количество вершин [math]n[/math]. Чтобы получить дерево из [math]n[/math] вершин достаточно взять [math]1[/math] вершину и подвесить к ней последовательность деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=S_{n-1}[/math].

[math]S_{n}=\sum_{i=1}^{n} T_{i} S_{n-i}=\sum_{i=1}^{n} S_{i-1} S_{n-i}=\sum_{i=0}^{n-1} S_{i} S_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана

Множества(PSet)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{n}\}[/math] — множество из различных объектов, [math]S=PSet(A)[/math] — множество всех множеств объектов, составленных из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{k}\}[/math] — количество объектов веса [math]\{1 \ldots k\}[/math], составленных из элементов [math]A[/math], [math]w_{0} = 1[/math]. Тогда количество множеств из объектов суммарного веса [math]n[/math] можно вычислить как [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}}{i} s_{n-ik, k-1}[/math] — количество таких множеств, что они содержат объекты суммарного веса [math]\leqslant k[/math].

Количество PSet из элементов [math]0[/math] или [math]1[/math]

Пусть [math]A={0, 1}[/math], [math]S=PSet(A)[/math] — множество всех множеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]w_{0} = 1[/math]. Тогда [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} s_{n-ik, k-1}[/math]

[math]S_{0}=s_{0, 0} = 1[/math]

[math]S_{1}=s_{1, 1} = s_{1, 0} + 2s_{0, 0} = 2s_{0, 0} = 2[/math]

[math]S_{2}=s_{2, 2} = s_{2, 1} + 0 \cdot s_{0, 1} = s_{2, 0} + 2s_{1, 0} + s_{0, 0}= s_{0, 0} = 1[/math]

[math]{S_{3}=s_{3, 3} = s_{3, 2} + 0 \cdot s_{0, 2} = s_{3, 1} + 0 \cdot s_{0, 1} = s_{3, 0} + 2s_{2, 0} + 0 \cdot s_{1, 0} + 0 \cdot s_{0, 0}= 0}[/math]

Для [math]n \gt 2[/math], [math]S_{n} = 0[/math]

[math]\{\}[/math]

[math]\{0\}, \{1\}[/math]

[math]\{0, 1\}[/math]

Количество разбиений на слагаемые

Пусть [math]A=\mathbb{N}[/math], [math]S=PSet(A)[/math] — множество всех разбиений на слагаемые, [math]W=\{1 \ldots 1\}[/math], [math]w_{0} = 1[/math]. Тогда,

[math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} s_{n-ik, k-1} = s_{n, k-1} + s_{n - k, k}[/math], что, как не сложно заметить, соответствует формуле, полученной методом динамического программирования.

Мультимножества(MSet)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{n}\}[/math] — множество из различных объектов, [math]S=MSet(A)[/math] — множество всех мультимножеств объектов, составленных из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{k}\}[/math] — количество объектов веса [math]\{1 \ldots k\}[/math], составленных из элементов [math]A[/math], [math]w_{0} = 1[/math]. Тогда количество мультимножеств из объектов суммарного веса [math]n[/math] можно вычислить как [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}+i-1}{i} s_{n-ik, k-1}[/math] — количество таких мультимножеств, что они содержат объекты суммарного веса не более [math]k[/math].

Количество MSet из элементов [math]0[/math] или [math]1[/math]

Пусть [math]A={0, 1}[/math], [math]S=PSet(A)[/math] — множество всех множеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]w_{0} = 1[/math].

Тогда, [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} s_{n-ik, k-1}[/math]

[math]S_{0}=s_{0, 0} = 1[/math]

[math]S_{1}=s_{1, 1} = s_{1, 0} + 2s_{0, 0} = 2s_{0, 0} = 2[/math]

[math]S_{2}=s_{2, 2} = s_{2, 1} + 0 \cdot s_{0, 1} = s_{2, 0} + 2s_{1, 0} + 3s_{0, 0}= 3s_{0, 0} = 3[/math]

[math]S_{3}=s_{3, 3} = s_{3, 2} + 0 \cdot s_{0, 2} = s_{3, 1} + 0 \cdot s_{0, 1} = s_{3, 0} + 2s_{2, 0} + 3s_{1, 0} + 4s_{0, 0}= 4s_{0, 0} = 4[/math]

[math]\{\}[/math]

[math]\{0\}, \{1\}[/math]

[math]\{0, 0\}, \{0, 1\}, \{1, 1\}[/math]

[math]\{0, 0, 0\}, \{0, 0, 1\}, \{0, 1, 1\}, \{1, 1, 1\}[/math]

[math]{S_{n}=s_{n, n} = s_{n, n-1} + 0 \cdot s_{0, n-1} = s_{n, n-2} + 0 \cdot s_{0, n-2} = \ldots = s_{n, 0} + 2s_{n - 1, 0} + \ldots + ns_{1, 0} + (n+1) s_{0,0} = (n + 1) s_{0,0} = n+1}[/math]

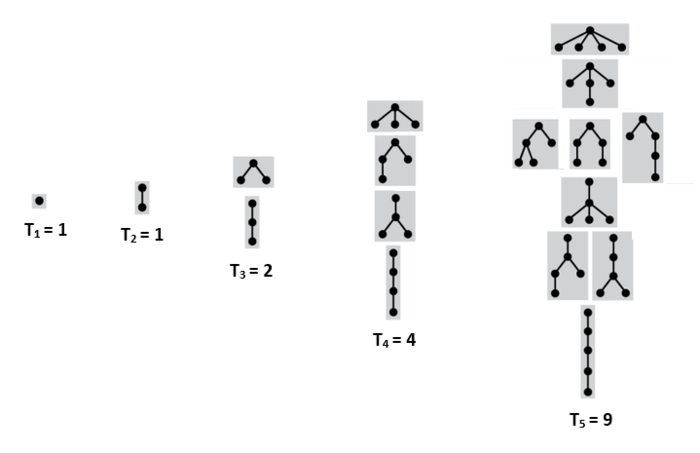
Подсчет подвешенных непомеченных деревьев без порядка на детях

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами, [math]T_{0} = 1[/math]. [math]F=MSet(T)[/math] — множество всех лесов из данных деревьев, так как лес можно интерпретировать как мультимножество из деревьев. [math]F_{n}=f_{n,n}[/math] — количество лесов с суммарным количество вершин [math]n[/math]. [math]f_{n, k}[/math] — количество лесов из [math]n[/math] вершин, таких что они содержат не более чем [math]k[/math] вершин. Чтобы получить дерево из [math]n[/math] вершин достаточно взять [math]1[/math] вершину и подвесить к ней лес деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=F_{n-1}[/math].

[math]F_{n}=f_{n, n}[/math].

[math]f{n,k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{T_{k}+i-1}{i} s_{n-ik, k-1}[/math]

Количество таких деревьев с [math]n[/math] вершинами образуют последовательность [math] 1, 1, 2, 4, 9, 20, 48, 115, 286, 719, 1842, 4766, 12486, 32973, 87811, 235381, 634847 \ldots[/math]

Пары(Pair)

Утверждение:

Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{n}\}[/math], [math]B=\{b_{1},b_{2}, \ldots ,b_{m}\}[/math] — множества из различных объектов, [math]S=Pair(A, B)[/math] — множество всех пар объектов, составленных из элементов [math]A[/math] и [math]B[/math]. [math]W=\{w_{1},w_{2}, \ldots ,w_{k}\}[/math] — количество объектов веса [math]\{1 \ldots k\}[/math], составленных из элементов [math]A[/math], а [math]U=\{u_{1},u_{2}, \ldots ,u_{k}\}[/math] — соответственно для [math]B[/math]. Тогда количество пар из объектов суммарного веса [math]n[/math] можно вычислить как [math]S_{n}=\sum_{i=0}^{n}w_{i}u_{n-i}[/math].

Количество подвешенных неполных двоичных деревьев

Пусть [math]T_{n}[/math] — количество таких деревьев с [math]n[/math] вершинами, [math]T_{0} = 1[/math]. [math]S=Pair(T, T)[/math] — множество всех пар из данных деревьев. Чтобы получить двоичное дерево из [math]n[/math] вершин, достаточно взять [math]1[/math] вершину и подвесить к ней левого и правого сына с суммарным количеством вершин [math]n-1[/math]. Тогда:

[math]T_{n}=S_{n-1}=\sum_{i=0}^{n-1}T_{i}T_{n-i-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана.