Алгоритм Куна для поиска максимального паросочетания — различия между версиями
(→Алгоритм) |
Rost (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
|statement= | |statement= | ||
Если из вершины <tex>x</tex> не существует дополняющей цепи относительно паросочетания <tex>M</tex>, то если паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи, то из <tex>x</tex> не существует дополняющей цепи в <tex>M'</tex>. | Если из вершины <tex>x</tex> не существует дополняющей цепи относительно паросочетания <tex>M</tex>, то если паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи, то из <tex>x</tex> не существует дополняющей цепи в <tex>M'</tex>. | ||
| − | |proof= | + | |proof= |
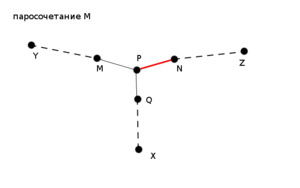
| + | [[Файл:Kuhn.png|thumb|left|300x300px|Пунктиром обозначено существование пути между двумя вершинами.]] | ||
}} | }} | ||
==Алгоритм== | ==Алгоритм== | ||
Версия 08:26, 15 января 2011
| Теорема: |
Если из вершины не существует дополняющей цепи относительно паросочетания , то если паросочетание получается из изменением вдоль дополняющей цепи, то из не существует дополняющей цепи в . |
| Доказательство: |
Содержание
Алгоритм
Пусть дан двудольный граф и требуется найти максимальное паросочетание в нём. Обозначим доли исходного графа как и .
1) Просматриваем вершины из доли .
2) Будем искать дополняющую цепь из (например, поиском в глубину).
3) Если цепь найдена, инвертируем все ребра на этой цепи.
В любой момент времени текущим паросочетанием будет множество ребер, направленных из в . Корректность работы алгоритма следует из теоремы Бержа и доказанной выше теоремы.
Псевдокод
bool dfs(x): vis[x] = true for : k = py[y] if (k == -1) or ((not vis[k]) and (dfs(k))): py[y] = x return true return false Kuhn(): py[] = -1 for : vis[] = false dfs(s)
Время работы
Итак, алгоритм Куна можно представить как серию из || запусков обхода в глубину на всём графе. Следовательно, всего этот алгоритм исполняется за время , что в худшем случае есть .
Источники
Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010. — 291 стр.