Переобучение — различия между версиями
(→Примеры) |
|||
| Строка 4: | Строка 4: | ||
== Примеры == | == Примеры == | ||
| − | === На примере линейной регрессии === | + | === На примере линейной регрессии<ref>[[Линейная регрессия]]</ref> === |
Представьте задачу предсказания <math>y</math> по <math>x \in R</math>. Рис 1 показывает результат использования модели <math>y=θ_0+θ_1*x</math> для представленного датасета. Как видно из Рис 1 данные не поддаются линейной зависимости, и по этой причине модель не очень хороша. | Представьте задачу предсказания <math>y</math> по <math>x \in R</math>. Рис 1 показывает результат использования модели <math>y=θ_0+θ_1*x</math> для представленного датасета. Как видно из Рис 1 данные не поддаются линейной зависимости, и по этой причине модель не очень хороша. | ||
{|align="center" | {|align="center" | ||
| Строка 14: | Строка 14: | ||
Если же добавить дополнительный параметр <math>x^2</math>, и использовать модель <math>y=θ_0+θ_1*x+θ_2*x^2</math>, как представлено на Рис 2, то модель значительно лучше подходит для представленного датасета. Рис 3 показывает результат использования модели <math>y=θ_0+θ_1*x+θ_2*x^2+θ_3*x^3+θ_4*x^4</math> для представленного датасета. Как видно из Рис 3 данная модель слишком заточена для точки обучающего датасета и, веротяно, покажет плохой результат на тестовом датасете. | Если же добавить дополнительный параметр <math>x^2</math>, и использовать модель <math>y=θ_0+θ_1*x+θ_2*x^2</math>, как представлено на Рис 2, то модель значительно лучше подходит для представленного датасета. Рис 3 показывает результат использования модели <math>y=θ_0+θ_1*x+θ_2*x^2+θ_3*x^3+θ_4*x^4</math> для представленного датасета. Как видно из Рис 3 данная модель слишком заточена для точки обучающего датасета и, веротяно, покажет плохой результат на тестовом датасете. | ||
| − | === На примере логистической регрессии === | + | === На примере логистической регрессии<ref>[[Логистическая регрессия]]</ref> === |
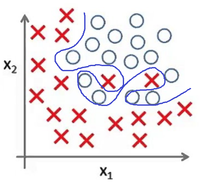
Представьте задачу классификации размеченых точек. Рис 4 показывает результат использования модели <math>g(θ_0+θ_1*x_1+θ_2*x_2)</math> для представленного датасета. Как и в предыдущем примере, данные не поддаются классификации по линейной зависимости. | Представьте задачу классификации размеченых точек. Рис 4 показывает результат использования модели <math>g(θ_0+θ_1*x_1+θ_2*x_2)</math> для представленного датасета. Как и в предыдущем примере, данные не поддаются классификации по линейной зависимости. | ||
{|align="center" | {|align="center" | ||
| Строка 22: | Строка 22: | ||
|[[Файл:High_variance_cla.png|200px|thumb|Рис 6. Переобучение]] | |[[Файл:High_variance_cla.png|200px|thumb|Рис 6. Переобучение]] | ||
|} | |} | ||
| − | В случае же выбора модели <math>g(θ_0+θ_1*x_1+θ_2*x_2+θ_3*x_1^2+θ_4*x_2^2+θ_5*x_1*x_2)</math>, представленой на Рис 5, данные значительно лучше соответствуют модели. Рис 6 показывает результат использования модели <math>g(θ_0+θ_1*x_1+θ_2*x_1^2+θ_3*x_2*x_1^2+θ_4*x_1^2*x_2^2 + ...)</math> для представленного датасета {{---}} это яркий пример явления переобучения. | + | В случае же выбора модели <math>g(θ_0+θ_1*x_1+θ_2*x_2+θ_3*x_1^2+θ_4*x_2^2+θ_5*x_1*x_2)</math>, представленой на Рис 5, данные значительно лучше соответствуют модели. Рис 6 показывает результат использования модели <math>g(θ_0+θ_1*x_1+θ_2*x_1^2+θ_3*x_2*x_1^2+θ_4*x_1^2*x_2^2 + ...)</math> для представленного датасета {{---}} это яркий пример явления переобучения. |
== Кривые обучения == | == Кривые обучения == | ||
Версия 18:28, 14 декабря 2018
Переобучение (англ. overfitting) — негативное явление, возникающее, когда алгоритм обучения вырабатывает предсказания, которые слишком близко или точно соответствуют конкретному набору данных, и поэтому не подходят для применения алгоритма к дополнительным данным или будущим наблюдениям.
Недообучение (англ. underfitting) — негативное явление, при котором алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.
Содержание
Примеры
На примере линейной регрессии[1]
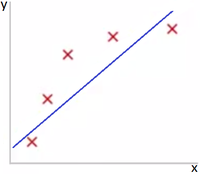
Представьте задачу предсказания по . Рис 1 показывает результат использования модели для представленного датасета. Как видно из Рис 1 данные не поддаются линейной зависимости, и по этой причине модель не очень хороша.
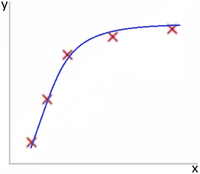
Если же добавить дополнительный параметр , и использовать модель , как представлено на Рис 2, то модель значительно лучше подходит для представленного датасета. Рис 3 показывает результат использования модели для представленного датасета. Как видно из Рис 3 данная модель слишком заточена для точки обучающего датасета и, веротяно, покажет плохой результат на тестовом датасете.
На примере логистической регрессии[2]
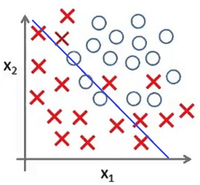
Представьте задачу классификации размеченых точек. Рис 4 показывает результат использования модели для представленного датасета. Как и в предыдущем примере, данные не поддаются классификации по линейной зависимости.
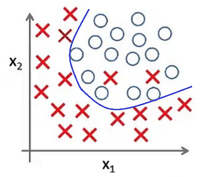
В случае же выбора модели , представленой на Рис 5, данные значительно лучше соответствуют модели. Рис 6 показывает результат использования модели для представленного датасета — это яркий пример явления переобучения.
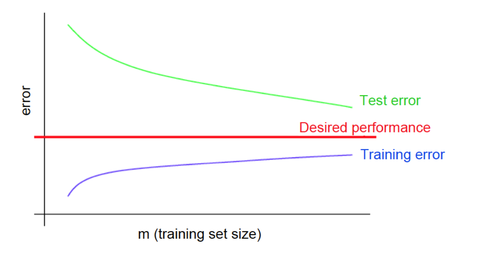
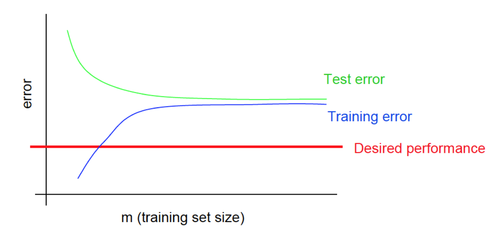
Кривые обучения
Кривые обучения при переобучении
Кривые обучения при недообучении
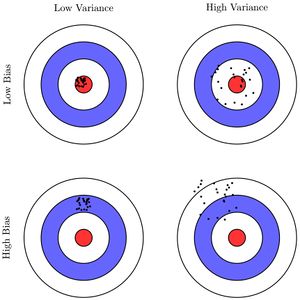
High variance и high bias
Bias — ошибка неверных предположений в алгоритме обучения. Высокий bias может привести к недообучению.
Variance — это ошибка, вызванная большой чувствительностью к небольшим отклонениям в тренировочном наборе. Высокая дисперсия может привести к переобучению.
При использовании нейронных сетей variance увеличивается, а bias уменьшается с увеличением количества скрытых слоев.
Для устранения high variance и high bias можно использовать смеси и ансамбли. Например, можно составить ансамбль (boosting) из нескольких моделей с высоким bias и получить модель с небольшим bias. В другом случае при bagging соединяются несколько моделей с низким bias, а результирующая модель позволяет уменьшить variance.
Возможные решения
Возможные решения при переобучении
- Увеличение количества данных в наборе
- Уменьшение количества параметров модели
- Добавление регуляризации / увеличение коэффициента регуляризации
Возможные решения при недообучении
- Добавление новых параметров модели
- Использование для описания модели функций с более высокой степенью
- Уменьшение коэффициента регуляризации
См. также
- Модель алгоритма и ее выбор[на 01.12.18 не создан]
- Оценка качества в задачах классификации и регрессии[на 01.12.18 не создан]
- Оценка качества в задаче кластеризации[на 01.12.18 не создан]
- The Problem of Overfitting on Coursera, Andrew Ng
Примечания
- Overfitting: when accuracy measure goes wrong
- The Problem of Overfitting Data
- Overfitting in Machine Learning
Источники информации
- Overfitting - статься на Википедии
- Переобучение - вводная статься на MachineLearning.ru
- The Problem of Overfitting - курс Andrew Ng
- Hastie, T., Tibshirani, R., Friedman, J. The Elements of Statistical Learning, 2nd edition. — Springer, 2009. — 533 p.
- Vapnik V.N. Statistical learning theory. — N.Y.: John Wiley & Sons, Inc., 1998.
- Воронцов, К. В. Комбинаторная теория надёжности обучения по прецедентам: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр РАН, 2010. — 271 с.