Сверточные нейронные сети — различия между версиями
| Строка 2: | Строка 2: | ||
== Свертка == | == Свертка == | ||
| − | [[Файл:Convolution_example.png|upright=1. | + | [[Файл:Convolution_example.png|upright=1.0|thumb|Пример свертки двух матриц размера 5x5 и 3x3]] |
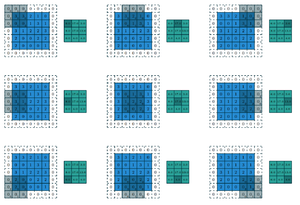
'''Свертка''' (англ. ''convolution'') {{---}} операция над парой матриц <math>A</math> (размера <math>n_x\times n_y</math>) и <math>B</math> (размера <math>m_x \times m_y</math>), результатом которой является матрица <math>C = A * B</math> размера <math>(n_x-m_x+1)\times (n_y-m_y+1)</math>. | '''Свертка''' (англ. ''convolution'') {{---}} операция над парой матриц <math>A</math> (размера <math>n_x\times n_y</math>) и <math>B</math> (размера <math>m_x \times m_y</math>), результатом которой является матрица <math>C = A * B</math> размера <math>(n_x-m_x+1)\times (n_y-m_y+1)</math>. | ||
Каждый элемент результата вычисляется как скалярное произведение матрицы <math>B</math> и некоторой подматрицы <math>A</math> такого же размера (подматрица определяется положением элемента в результате). | Каждый элемент результата вычисляется как скалярное произведение матрицы <math>B</math> и некоторой подматрицы <math>A</math> такого же размера (подматрица определяется положением элемента в результате). | ||
| Строка 10: | Строка 10: | ||
== Структура сверточной нейронной сети == | == Структура сверточной нейронной сети == | ||
| − | В сверточной нейронной сети выходы промежуточных слоев образуют матрицу (изображение) или набор матриц (несколько слоёв изображения). Так, например, на вход сверточной нейронной сети можно подавать три слоя изображения (R-, G-, B-каналы изображения). | + | В сверточной нейронной сети выходы промежуточных слоев образуют матрицу (изображение) или набор матриц (несколько слоёв изображения). Так, например, на вход сверточной нейронной сети можно подавать три слоя изображения (R-, G-, B-каналы изображения). Основными видами слоев в сверточной нейронной сети являются сверточные слои (англ. ''convolutional layer''), пулинговые слои (англ. ''pooling layer'') и [[:Нейронные сети, перцептрон|полносвязные слои]]<sup>[на 09.01.19 не создан]</sup> (англ. ''fully-connected layer''). |
=== Сверточный слой === | === Сверточный слой === | ||
| − | [[Файл:Padding.png|upright=1. | + | [[Файл:Padding.png|upright=1.0|thumb|Пример свертки двух матриц с дополнением нулями и сдвигом 2]] |
| − | Сверточный слой нейронной сети представляет из себя применение операции свертки к выходам с предыдущего слоя, где веса ядра свертки являются обучаемыми параметрами. Еще один обучаемый вес используется в качестве константного сдвига (англ. bias). При этом есть несколько важных деталей: | + | [[Файл:Convolution-operation-on-volume5.png|upright=1.0|thumb|Пример свертки с трехмерным ядром]] |
| + | Сверточный слой нейронной сети представляет из себя применение операции свертки к выходам с предыдущего слоя, где веса ядра свертки являются обучаемыми параметрами. Еще один обучаемый вес используется в качестве константного сдвига (англ. ''bias''). При этом есть несколько важных деталей: | ||
* В одном сверточном слое может быть несколько сверток. В этом случае для каждой свертки на выходе получится своё изображение. Например, если вход имел размерность <math>w\times h</math>, а в слое было <math>n</math> сверток с ядром размерности <math>k_x\times k_y</math>, то выход будет иметь размерность <math>n\times(w - k_x + 1)\times(h - k_y + 1)</math>. | * В одном сверточном слое может быть несколько сверток. В этом случае для каждой свертки на выходе получится своё изображение. Например, если вход имел размерность <math>w\times h</math>, а в слое было <math>n</math> сверток с ядром размерности <math>k_x\times k_y</math>, то выход будет иметь размерность <math>n\times(w - k_x + 1)\times(h - k_y + 1)</math>. | ||
| Строка 20: | Строка 21: | ||
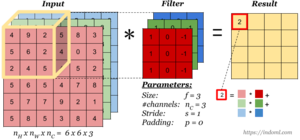
* Ядра свертки могут быть трёхмерными. Свертка трехмерного входа с трехмерным ядром происходит аналогично, просто скалярное произведение считается еще и по всем слоям изображения. Например, для усреднения информации о цветах исходного изображения, на первом слое можно использовать свертку размерности <math>3\times w \times h</math>. На выходе такого слоя будет уже одно изображение (вместо трёх). | * Ядра свертки могут быть трёхмерными. Свертка трехмерного входа с трехмерным ядром происходит аналогично, просто скалярное произведение считается еще и по всем слоям изображения. Например, для усреднения информации о цветах исходного изображения, на первом слое можно использовать свертку размерности <math>3\times w \times h</math>. На выходе такого слоя будет уже одно изображение (вместо трёх). | ||
| − | * Можно заметить, что применение операции свертки уменьшает изображение. Также пиксели, которые находятся на границе изображения учавствуют в меньшем количестве сверток, чем внутренние. В связи с этим в сверточных слоях используется дополнение изображения (англ. padding). Выходы с предыдущего слоя дополняются пикселями так, чтобы после свертки сохранился размер изображения (распространенной практикой является дополнять изображение нулями (англ. zero padding), но возможны и другие подходы). Такие свертки называют ''одинаковыми'' (англ. same convolution), а свертки без дополнения изображения называются ''правильными'' (англ. valid convolution). | + | * Можно заметить, что применение операции свертки уменьшает изображение. Также пиксели, которые находятся на границе изображения учавствуют в меньшем количестве сверток, чем внутренние. В связи с этим в сверточных слоях используется дополнение изображения (англ. ''padding''). Выходы с предыдущего слоя дополняются пикселями так, чтобы после свертки сохранился размер изображения (распространенной практикой является дополнять изображение нулями (англ. ''zero padding''), но возможны и другие подходы). Такие свертки называют ''одинаковыми'' (англ. ''same convolution''), а свертки без дополнения изображения называются ''правильными'' (англ. ''valid convolution''). |
| − | * Еще одним параметром сверточного слоя является ''сдвиг'' (англ. stride). Хоть обычно свертка применяется подряд для каждого пикселя, иногда используется сдвиг, отличный от единицы {{---}} скалярное произведение считается не со всеми возможными положениями ядра, а только с положениями, кратными некоторому сдвигу <math>s</math>. Тогда, если если вход имел размерность <math>w\times h</math>, а ядро свертки имело размерность <math>k_x\times k_y</math> и использовался сдвиг <math>s</math>, то выход будет иметь размерность <math>\lfloor\frac{w - k_x}{s} + 1\rfloor\times\lfloor\frac{h - k_y}{s} + 1\rfloor</math>. | + | * Еще одним параметром сверточного слоя является ''сдвиг'' (англ. ''stride''). Хоть обычно свертка применяется подряд для каждого пикселя, иногда используется сдвиг, отличный от единицы {{---}} скалярное произведение считается не со всеми возможными положениями ядра, а только с положениями, кратными некоторому сдвигу <math>s</math>. Тогда, если если вход имел размерность <math>w\times h</math>, а ядро свертки имело размерность <math>k_x\times k_y</math> и использовался сдвиг <math>s</math>, то выход будет иметь размерность <math>\lfloor\frac{w - k_x}{s} + 1\rfloor\times\lfloor\frac{h - k_y}{s} + 1\rfloor</math>. |
=== Пулинговый слой === | === Пулинговый слой === | ||
| − | Пулинговый слой призван снижать размерность изображения. Исходное изображение делится на блоки размером <math>w\times h</math> и для каждого блока вычисляется некоторая функция ( | + | [[Файл:Maxpool.jpeg|upright=1.0|thumb|Пример операции пулинга с функцией максимума]] |
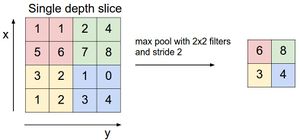
| + | Пулинговый слой призван снижать размерность изображения. Исходное изображение делится на блоки размером <math>w\times h</math> и для каждого блока вычисляется некоторая функция. Чаще всего используется функция максимума (англ. ''max pooling'') или (взвешенного) среднего (англ. ''(weighted) average pooling''). Обучаемых параметров у этого слоя нет. Основные цели пулингового слоя: | ||
| + | * уменьшение изображения, чтобы последующие свертки оперировали над большей областью исходного изображения; | ||
| + | * увеличение инвариантности выхода сети по отношению к малому переносу входа; | ||
| + | * ускорение вычислений. | ||
| + | |||
| + | == Известные архитектуры сверточных нейронных сетей == | ||
| + | === LeNet-5 === | ||
| + | [[Файл:Lenet5.png|upright=1.0|thumb|Архитектура LeNet-5]] | ||
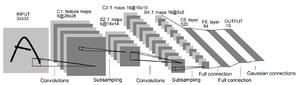
| + | Нейронная сеть, предложенная Яном Лекуном, для распознавания рукописных цифр MNIST. | ||
| + | |||
| + | === AlexNet === | ||
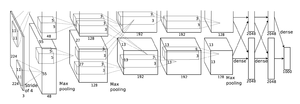
| + | [[Файл:Alexnet.png|upright=1.0|thumb|Архитектура AlexNet]] | ||
| + | Победитель соревнования ImageNet 2012-ого года, набравший точность 84.6%. Была реализована с использованием CUDA для повышения производительности. Состоит из двух отдельных частей, которые слабо взаимодействуют друг с другом, что позволяет исполнять их параллельно на разных GPU с минимальным обменом данными. | ||
| + | |||
| + | === VGG === | ||
| + | Семейство архитектур нейронных сетей, которое включает в себя, в частности, VGG-11, VGG-13, VGG-16 и VGG-19. Победитель соревнования ImageNet 2013-ого года (VGG-16), набравший точность 92.7%. Одной из отличительных особенностей является использование ядер свертки небольшого размера (3x3, в отличие от больших ядер размера 7x7 или 11x11). | ||
Версия 14:57, 10 января 2019
Сверточная нейронная сеть (англ. convolutional neural network, CNN) — специальная архитектура нейронных сетей, предложенная Яном Лекуном, изначально нацеленная на эффективное распознавание изображений.
Содержание
Свертка
Свертка (англ. convolution) — операция над парой матриц (размера ) и (размера ), результатом которой является матрица размера . Каждый элемент результата вычисляется как скалярное произведение матрицы и некоторой подматрицы такого же размера (подматрица определяется положением элемента в результате). То есть, . На изображении справа можно видеть, как матрица «двигается» по матрице , и в каждом положении считается скалярное произведение матрицы и той части матрицы , на которую она сейчас наложена. Получившееся число записывается в соответствующий элемент результата.
Логический смысл свертки такой — чем больше величина элемента свертки, тем больше эта часть матрицы была похожа на матрицу (похожа в смысле скалярного произведения). Поэтому матрицу называют изображением, а матрицу — фильтром или образцом.
Структура сверточной нейронной сети
В сверточной нейронной сети выходы промежуточных слоев образуют матрицу (изображение) или набор матриц (несколько слоёв изображения). Так, например, на вход сверточной нейронной сети можно подавать три слоя изображения (R-, G-, B-каналы изображения). Основными видами слоев в сверточной нейронной сети являются сверточные слои (англ. convolutional layer), пулинговые слои (англ. pooling layer) и полносвязные слои[на 09.01.19 не создан] (англ. fully-connected layer).
Сверточный слой
Сверточный слой нейронной сети представляет из себя применение операции свертки к выходам с предыдущего слоя, где веса ядра свертки являются обучаемыми параметрами. Еще один обучаемый вес используется в качестве константного сдвига (англ. bias). При этом есть несколько важных деталей:
- В одном сверточном слое может быть несколько сверток. В этом случае для каждой свертки на выходе получится своё изображение. Например, если вход имел размерность , а в слое было сверток с ядром размерности , то выход будет иметь размерность .
- Ядра свертки могут быть трёхмерными. Свертка трехмерного входа с трехмерным ядром происходит аналогично, просто скалярное произведение считается еще и по всем слоям изображения. Например, для усреднения информации о цветах исходного изображения, на первом слое можно использовать свертку размерности . На выходе такого слоя будет уже одно изображение (вместо трёх).
- Можно заметить, что применение операции свертки уменьшает изображение. Также пиксели, которые находятся на границе изображения учавствуют в меньшем количестве сверток, чем внутренние. В связи с этим в сверточных слоях используется дополнение изображения (англ. padding). Выходы с предыдущего слоя дополняются пикселями так, чтобы после свертки сохранился размер изображения (распространенной практикой является дополнять изображение нулями (англ. zero padding), но возможны и другие подходы). Такие свертки называют одинаковыми (англ. same convolution), а свертки без дополнения изображения называются правильными (англ. valid convolution).
- Еще одним параметром сверточного слоя является сдвиг (англ. stride). Хоть обычно свертка применяется подряд для каждого пикселя, иногда используется сдвиг, отличный от единицы — скалярное произведение считается не со всеми возможными положениями ядра, а только с положениями, кратными некоторому сдвигу . Тогда, если если вход имел размерность , а ядро свертки имело размерность и использовался сдвиг , то выход будет иметь размерность .
Пулинговый слой
Пулинговый слой призван снижать размерность изображения. Исходное изображение делится на блоки размером и для каждого блока вычисляется некоторая функция. Чаще всего используется функция максимума (англ. max pooling) или (взвешенного) среднего (англ. (weighted) average pooling). Обучаемых параметров у этого слоя нет. Основные цели пулингового слоя:
- уменьшение изображения, чтобы последующие свертки оперировали над большей областью исходного изображения;
- увеличение инвариантности выхода сети по отношению к малому переносу входа;
- ускорение вычислений.
Известные архитектуры сверточных нейронных сетей
LeNet-5
Нейронная сеть, предложенная Яном Лекуном, для распознавания рукописных цифр MNIST.
AlexNet
Победитель соревнования ImageNet 2012-ого года, набравший точность 84.6%. Была реализована с использованием CUDA для повышения производительности. Состоит из двух отдельных частей, которые слабо взаимодействуют друг с другом, что позволяет исполнять их параллельно на разных GPU с минимальным обменом данными.
VGG
Семейство архитектур нейронных сетей, которое включает в себя, в частности, VGG-11, VGG-13, VGG-16 и VGG-19. Победитель соревнования ImageNet 2013-ого года (VGG-16), набравший точность 92.7%. Одной из отличительных особенностей является использование ядер свертки небольшого размера (3x3, в отличие от больших ядер размера 7x7 или 11x11).