Выброс — различия между версиями
Fest (обсуждение | вклад) м (→Методы обнаружения и борьбы с выбросами) |
Fest (обсуждение | вклад) м (→Алгоритмы борьбы с выбросами) |
||
| Строка 31: | Строка 31: | ||
===Алгоритмы борьбы с выбросами=== | ===Алгоритмы борьбы с выбросами=== | ||
| − | * Локально взвешенное сглаживание(англ. ''LOcally WEighted Scatter plot Smoothing'', ''LOWESS'')<ref>http://www.aliquote.org/cours/2012_biomed/biblio/Cleveland1979.pdf</ref>. | + | * Локально взвешенное сглаживание(англ. ''LOcally WEighted Scatter plot Smoothing'', ''LOWESS'')<ref>[http://www.aliquote.org/cours/2012_biomed/biblio/Cleveland1979.pdf Локально взвешенное сглаживание]</ref>. |
ВХОД: <math>X^\ell</math> (-) обучающая выборка; | ВХОД: <math>X^\ell</math> (-) обучающая выборка; | ||
ВЫХОД: коэффиценты <math>\gamma_i, i = 1,...,\ell</math>; | ВЫХОД: коэффиценты <math>\gamma_i, i = 1,...,\ell</math>; | ||
| Строка 43: | Строка 43: | ||
6: <math>\gamma_i := \widetilde{K}\left (\left | a_i-y_i \right | \right );</math> | 6: <math>\gamma_i := \widetilde{K}\left (\left | a_i-y_i \right | \right );</math> | ||
7: пока коэффиценты <math>\gamma_i</math> не стабилизируются; | 7: пока коэффиценты <math>\gamma_i</math> не стабилизируются; | ||
| − | Пример. Допустим мы пытаемся восстановить зависимость, используя ''формулу Надарая-Ватсона''<ref>http://www.machinelearning.ru/wiki/index.php?title=%D0%9E%D1%86%D0%B5%D0%BD%D0%BA%D0%B0_%D0%9D%D0%B0%D0%B4%D0%B0%D1%80%D0%B0%D1%8F-%D0%92%D0%B0%D1%82%D1%81%D0%BE%D0%BD%D0%B0</ref> по некоторым данным из n наблюдений, 2 из которых имеют излишне высокое и излишне низкое значения соответственно. Большие ошибки, вызванные этими выбросами, довольно заметно исказят полученный результат по формуле. В методе локально взвешенного сглаживания мы домножаем веса объектов <math>w_i</math> на коэффиценты <math>\gamma_i=\widetilde{K}\left(\varepsilon_i\right)</math>, значения которых тем меньше, чем величина ошибки <math>\varepsilon_i</math>. Для этого мы возьмём квартическое ядро (не обязательно совпадающее с основным ядром) <math>\widetilde{K}\left(\varepsilon\right)=K_Q\left(\frac{\varepsilon}{6Me\left\{\varepsilon_i\right\}}\right)</math>, где <math>Me\left \{\varepsilon_i\right \}</math> — медиана множества значений <math>\varepsilon_i</math>. | + | Пример. Допустим мы пытаемся восстановить зависимость, используя ''формулу Надарая-Ватсона''<ref>[http://www.machinelearning.ru/wiki/index.php?title=%D0%9E%D1%86%D0%B5%D0%BD%D0%BA%D0%B0_%D0%9D%D0%B0%D0%B4%D0%B0%D1%80%D0%B0%D1%8F-%D0%92%D0%B0%D1%82%D1%81%D0%BE%D0%BD%D0%B0 Формула Надарая-Ватсона]</ref> по некоторым данным из n наблюдений, 2 из которых имеют излишне высокое и излишне низкое значения соответственно. Большие ошибки, вызванные этими выбросами, довольно заметно исказят полученный результат по формуле. В методе локально взвешенного сглаживания мы домножаем веса объектов <math>w_i</math> на коэффиценты <math>\gamma_i=\widetilde{K}\left(\varepsilon_i\right)</math>, значения которых тем меньше, чем величина ошибки <math>\varepsilon_i</math>. Для этого мы возьмём квартическое ядро (не обязательно совпадающее с основным ядром) <math>\widetilde{K}\left(\varepsilon\right)=K_Q\left(\frac{\varepsilon}{6Me\left\{\varepsilon_i\right\}}\right)</math>, где <math>Me\left \{\varepsilon_i\right \}</math> — медиана множества значений <math>\varepsilon_i</math>. |
Таким образом выбросы будут нивелироваться автоматически при использовании данного подхода. В статистике методы, устойчивые к нарушениям модельных предположений о данных, называются ''робастными''. Метод локально взвешенного сглаживания относится к ''робастным'' методам, так как он устойчив к наличию небольшого количества выбросов. | Таким образом выбросы будут нивелироваться автоматически при использовании данного подхода. В статистике методы, устойчивые к нарушениям модельных предположений о данных, называются ''робастными''. Метод локально взвешенного сглаживания относится к ''робастным'' методам, так как он устойчив к наличию небольшого количества выбросов. | ||
| − | * Дерево принятия решения (англ. ''decision tree''<ref>https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B9</ref>). Это дерево, как и уже описанный алгоритм локально взвешенного сглаживания, относится ''робастным'' методам. | + | * Дерево принятия решения (англ. ''decision tree''<ref>[https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B9 Дерево принятия решения]</ref>). Это дерево, как и уже описанный алгоритм локально взвешенного сглаживания, относится ''робастным'' методам. |
==См.также== | ==См.также== | ||
Версия 01:20, 23 января 2019
Выброс(англ. outlier) — небольшая доля объектов во входных данных, которая сильно выделяется из общей выборки. Многие алгоритмы машинного обучения чувствительны к разбросу и распределению значений атрибутов во входных данных. Соответственно выбросы во входных данных могут исказить и ввести в заблуждение процесс обучения алгоритмов машинного обучения, что приводит к увеличению времени обучения, снижению точности моделей и, в конечном итоге, к снижению результатов. Даже до подготовки предсказательных моделей на основе обучающих данных выбросы могут приводить к ошибочным представлениям и в дальнейшем к ошибочной интерпретации собранных данных.
Содержание
Причины возникновения выбросов
- Сбой работы оборудования
- Человеческий фактор
- Случайность
- Уникальные явления
- и др.
Примеры
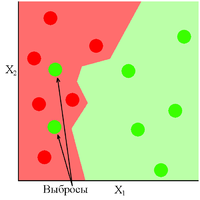
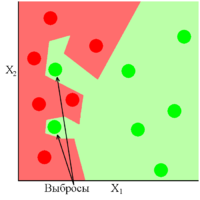
Рис 1 показывает хорошо обученную модель, в которой присутствуют два выброса. Как видно из рисунка данная модель показала себя устойчивой к выбросам, либо же вовремя прекратила своё обучение. Обратная ситуация обстоит с Рис 2, где модель сильно переобучилась из-за присутствующих в ней выбросов.
Методы обнаружения и борьбы с выбросами
Методы обнаружения выбросов
- Экстремальный анализ данных(англ. extreme value analysis). При таком анализе не применяются какие-либо специальные статистические методы. Обычно этот метод применим для одномерного случая. Алгоритм использования таков:
- Визуализировать данные, используя диаграммы и гистограммы для нахождения экстремальных значений.
- Задействовать распределение, например Гауссовское, и найти значения, чье стандартное отклонение отличается в 2-3 раза от математического ожидания или в полтора раза от первой либо третьей квартилей.
- Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели.
- Апроксимирующий метод (англ. proximity method). Чуть более сложный метод, заключающийся в применении кластеризующих методов.
- Использовать метод кластеризации для определения кластеров для данных.
- Идентифицировать и отметить центроиды каждого кластера.
- Соотнести кластеры с экземплярами данных, находящимися на фиксированном расстоянии или на процентном удалении от центроиды соответствующего кластера.
- Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели.
- Проецирующие методы (англ. projections methods). Эти методы довольно быстро и просто определяют выбросы в выборке.
- Использовать один из проецирующих методов, например метод главных компонент (англ. principal component analysis, PCA[1]) или самоорганизующиеся карты Кохонена(англ. self-organizing map, SOM[2]) или проекцию Саммона(англ. Sammon mapping, Sammon projection[3]), для суммирования обучающих данных в двух измерениях.
- Визуализировать отображение
- Использовать критерий близости от проецируемых значений или от вектора таблицы кодирования (англ. codebook vector) для идентифицирования выбросов.
- Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели.
Алгоритмы борьбы с выбросами
- Локально взвешенное сглаживание(англ. LOcally WEighted Scatter plot Smoothing, LOWESS)[4].
ВХОД: (-) обучающая выборка; ВЫХОД: коэффиценты ; ________________________________________________________ 1: инициализация: ; 2: повторять 3: для всех объектов ; 4: вычислить оценки скользящего контроля: 5: для всех объектов ; 6: 7: пока коэффиценты не стабилизируются;
Пример. Допустим мы пытаемся восстановить зависимость, используя формулу Надарая-Ватсона[5] по некоторым данным из n наблюдений, 2 из которых имеют излишне высокое и излишне низкое значения соответственно. Большие ошибки, вызванные этими выбросами, довольно заметно исказят полученный результат по формуле. В методе локально взвешенного сглаживания мы домножаем веса объектов на коэффиценты , значения которых тем меньше, чем величина ошибки . Для этого мы возьмём квартическое ядро (не обязательно совпадающее с основным ядром) , где — медиана множества значений . Таким образом выбросы будут нивелироваться автоматически при использовании данного подхода. В статистике методы, устойчивые к нарушениям модельных предположений о данных, называются робастными. Метод локально взвешенного сглаживания относится к робастным методам, так как он устойчив к наличию небольшого количества выбросов.
- Дерево принятия решения (англ. decision tree[6]). Это дерево, как и уже описанный алгоритм локально взвешенного сглаживания, относится робастным методам.
См.также
Примечания
- ↑ [1] Метод главных компонент]
- ↑ Самоорганизующиеся карты Кохонена
- ↑ Проекция Саммона
- ↑ Локально взвешенное сглаживание
- ↑ Формула Надарая-Ватсона
- ↑ Дерево принятия решения