Регуляризация

Определение:

Регуляризация (англ. regularization) в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить неккоректно поставленную задачу или предотвратить переобучение. Чаще всего эта информация имеет вид штрафа за сложность модели.

Мотивация

Как говорилось ранее, регуляризация полезна для борьбы с переобучением. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую.

На примере линейной регрессии

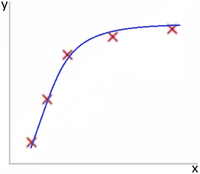
В качестве наглядного примера можно рассмотреть линейные регрессионные модели. Восстановить зависимость для нескольких точек можно пытаться полиномами разной степени M.

Рис 1. Норма. M=2

Рис 2. Переобучение. M=4

Как можно видеть на Рис 1. представлена зависимость, которая хорошо подходит для описания данных, а на Рис. 2 - модель слишком сильно заточилась под обучающую выборку.

Одним из способов бороться с этим эффектом - использовать регуляризацию, т. е. добавлять некоторый штраф за большие значения коэффициентов у линейной модели. Тем самым мы запретим слишком "резкие" изгибы и ограничим возможность подстраивания модели под данные.

На примере логистической регрессии

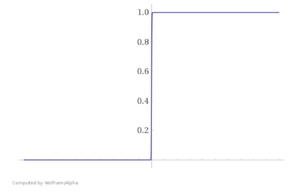
Необходимость регуляризации можно увидеть и на другом примере. Представьте, что ваша обучающая выборка была линейно разделима. В таком случае в процессе оптимизации значения весов уйдут в бесконечность и вместо сигмойды получится "ступенька", как представлено на Рис. 3.

Рис 3. Сигмойда - "ступенька"

Это плохо, ибо мы переобучились на нашу обучающую выборку. Как и в предыдущем примере, побороться с этим можно путем добавлением регуляризации, не дающей весам принимать слишком большие значения.

Основные виды регуляризации

Переобучение в большинстве случаев проявляется в том, что итоговые модели имеют слишком большие значения параметров. Соответственно, необходимо добавить в целевую функцию штраф за это. Наиболее часто используемые виды регуляризации - [math]L_{1}[/math] и [math]L_{2}[/math], а также их линейная комбинация - эластичная сеть.

В представленных ниже формулах для эмпирического риска [math]Q[/math]: [math]\mathcal{L}[/math] является функцией потерь, а [math]\beta[/math] - вектором параметров элемента [math]g(x, \beta)[/math] модели алгоритмов.

[math]L_{1}[/math]-регуляризация

[math]L_{1}[/math]-регуляризация (англ. lasso regression), или регуляризация через манхэттенское расстояние: [math]Q(\beta, X^l)=\sum _{i}\mathcal{L}(\beta, x_{i})+\lambda \sum _{j}{|\beta_{j}|}[/math].

[math]L_{2}[/math]-регуляризация

[math]L_{2}[/math]-регуляризация, или регуляризация Тихонова (англ. ridge regression или Tikhonov regularization): [math]Q(\beta, X^l)=\sum _{i}\mathcal{L}(\beta, x_{i})+\lambda \sum _{j}{\beta_{j}}^{2}[/math].

Эластичная сеть

Эластичная сеть (англ. elastic net regularization): [math]Q(\beta, X^l)=\sum _{i}\mathcal{L}(\beta, x_{i})+\lambda_{1} \sum _{j}{|\beta_{j}|}+\lambda_{2} \sum _{j}{\beta_{j}}^{2}[/math].