Рекомендательные системы

Рекомендательные системы — программы, которые пытаются предсказать, какие объекты будут интересны пользователю, имея определенную информацию о его профиле.

Обзор и постановка задачи

Основная задача рекомендательных систем — проинформировать пользователя о товаре или услуге, которая будет для него наиболее инетерсной и акутальной. Разнообразие таких систем можно проиллюстрировать основными характеристиками:

• Предмет рекомендации.
• Цель рекомендации.
• Контекст рекомендации.
• Источник рекомендации.
• Степень персонализации.
• Прозрачность.
• Формат рекомендации.
• Алгоритмы.

В центре таких систем лежит матрица предпочтений. В этой матрице одна из осей отвечает за пользователей, вторая за обхекты рекомендации. Заполнена же эта матрица значениями по заданной шкале (например от 1 до 5). Каждый клиент с малой долей вероятностью оценивал все объекты рекомендации, поэтому задача системы — это обобщение информации и предсказание, какое отношение к рекомендуемому обхекту будет у пользователя.

Пользовательские оценки, необходимые для составления матрицы предпочтений, можно получить двумя способами:

• явно (explicit ratings)
• неявно (implicit ratings)

Очевидно, что явное оценивание лучше, так как сам пользователь определяет насколько ему интересен тот или иной объект, однако из-за непостоянства в получении явных оценок от пользователей, на практике используется оба подхода.

Формализуем задачу. Имеется множество пользователей [math] u \in U [/math], множество объектов [math] i \in I [/math] и множество событий [math] (r_{ui}, u, i, ...) \in D [/math] (действия, которые совершают пользователи с объектами). Каждое событие задается пользователем [math] u [/math], объектом [math] i [/math], своим результатом [math] r_{ui} [/math] и, возможно, но не обяхательно, другими харакетристиками. По итогу требуется:

• предсказать предпочтение: [math] \hat{r}_{ui} = Predict(u, i, ...) \approx r_{ui} [/math]
• персональные рекомендации: [math] u \mapsto (i_1, ..., i_k) = Recommend_k(u, ...) [/math]
• похожие объекты: [math] u \mapsto (i_1, ..., i_M) = Similar_M(i) [/math]

Кластеризация пользователей

Определение:

Коллаборативная фильтрация (англ. collaborative filtering) — это один из методов построения прогнозов (рекомендаций) в рекомендательных системах, использующий известные предпочтения (оценки) группы пользователей для прогнозирования неизвестных предпочтений другого пользователя.

Основная идея метода — похожим пользователям нравятся похожие объекты.

Алгоритм можно разбить на следующие шаги:

• Выберем условную меру схожести пользователей по истории их оценок [math] sim(u, v) [/math]
• Объеденим пользователей в группы так, чтобы похожие пользователи оказывались в одном кластере [math] u \mapsto F(u) [/math]
• Оценку пользователя предскажем как среднюю оценку кластера этому объекту [math] \hat{r}_{ui} = \frac{1}{|F(u)|}\sum_{u \in F(u)}{}{r_{ui}} [/math]

Проблемы алгоритма:

• Нечего рекомендовать новым пользователям, их невозможно определить к какому-нибудь кластеру, а значит и рекомендовать им нечего.
• Не учитывается контекст и специфика пользователя.
• Если в кластере нет оценки объекта, то предсказание невозможно.

Холодный старт

Определение:

Холодный старт — ситуация, когда ещё не накоплено достаточное количество данных для корректной работы рекомендательной системы.

Данная проблема актуальна для новых объектов или объектов, которые редко покупают. Если средний рейтинг посчитан по оценкам всего трёх пользователей, такая оценка явно не будет достоверной, и пользователи это понимают. Часто в таких ситуациях рейтинги искусственно корректируют.

Первый способ – показывать не среднее значение, а сглаженное среднее (Damped Mean). Смысл таков: при малом количестве оценок отображаемый рейтинг больше тяготеет к некому безопасному «среднему» показателю, а как только набирается достаточное количество новых оценок, «усредняющая» корректировка перестает действовать.

Другой подход – рассчитывать по каждому рейтингу интервалы достоверности (Confidence Intervals). Математически, чем больше оценок, тем меньше вариация среднего и, значит, больше уверенность в его корректности. А в качестве рейтинга можно выводить, например, нижнюю границу интервала (Low CI Bound). При этом понятно, что такая система будет достаточно консервативной, с тенденцией к занижению оценок по новым товарам.

User-based и item-based алгоритмы

Заменим жесткую кластеризацию на предположение, что фильм понравится пользователю, если он понравился его друзьям.

[math] \hat{r}_{ui} = \bar{r}_u + \frac{\sum_{v \in U_i}{}{sim(u, v)(r_{vi} - \bar{r}_v)}}{\sum_{v \in {U_i}}{}{sim(u, v)}} [/math]

Однако у этого алгоритма есть недостатки:

• Холодный старт.
• Нечего рекомендовать новым/нетипичным пользователям.

Так же имеется абсолютно симметричный алгоритм. Теперь будем считать, что фильм понравится пользователю, если ему понравились похожие фильмы.

[math] \hat{r}_{ui} = \bar{r}_i + \frac{\sum_{j \in I_u}{}{sim(i, j)(r_{uj} - \bar{r}_j)}}{\sum_{j \in {I_u}}{}{sim(i, j)}} [/math]

У такого подхода остается недостаток в виде холодного старта и при этом рекомендации становятся тривиальными.

Так же стоит отметить ресурсоемкость вычислений такими методами. Для предсказаний необходимо держать в памяти все оценки всех пользователей.

Алгоритм SVD

Определение:

SVD (Single Value Decomposition) — у любой матрицы [math] A [/math] размера [math] n \times m [/math] существует разложение трех матриц: [math] U, \Sigma, V^T [/math]. Матрицы [math] U, V [/math] ортогональные, а [math] \Sigma [/math] — диагональная. [math] A_{n \times m} = U_{n \times n} \times \Sigma_{n \times m} \times V^T_{m \times m} [/math]

SVD для рекомендательных систем.

[math] UU^T = I_n[/math], [math]VV^T = I_m[/math]

[math] \Sigma = diag(\lambda_1, ..., \lambda_{min(n, m)})[/math], [math]\lambda_1 \geq ... \geq \lambda_{min(n, m)} \geq 0 [/math]

Обратить внимание же стоит на усеченное разложение, когда из лямбд, остаются только первые [math] d [/math] чисел, а остальные полагаем, что равны нулю.

[math] \lambda_{d+1}, ..., \lambda_{min(n,m)} := 0 [/math]

Значит у матриц [math] U [/math] и [math] V [/math] остаются только первые [math] d [/math] столбцов, а матрица [math] \Sigma [/math] становится квадратной размером [math] d \times d [/math].

[math] A'_{n \times m} = U'_{n \times d} \times \Sigma'_{d \times d} \times V'^T_{d \times m} [/math]

Получаем наилучшее низкоранговое приближение с точки зрения средне-квадратичного отклонения.

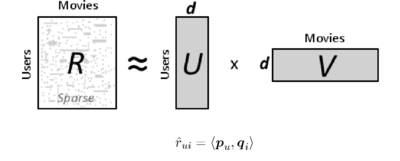
Чтобы предсказать оценку пользователя [math] U [/math] для объекта [math] I [/math], берём некотрый вектор [math] p_u [/math] для данного пользователя и вектор данного объекта [math] q_i [/math]. Получаем необходимое предсказание: [math] \hat{r}_{ui} = \langle p_u,q_i \rangle [/math].

Помимо предсказания оценок, алгоритм позволяет выявлять скрытые признаки объектов и интересы пользователей.

Одна есть и свои проблемы:

• [math] R [/math] матрица оценок полностью не известна, поэтому просто взять SVD разложение не получится.
• SVD разложение не единственное, поэтому даже если какое-то разложение будет найдено, нет гарантии, что первая координата в нем будет соответствовать некоторым выбранным характеристикам пользователя.

Решение проблемы матрицы оценок

Модель будет зависить от ногих параметров — вектора пользователей и вектора объектов. Для заданных парметров, возьмем вектор пользователя, вектор объекта и получим их скалярное произведение, чтобы предсказать оценку:

[math] \hat{r}_{ui}(\Theta) = p^T_uq_i [/math],

[math] \Theta = {p_u,q_i | u \in U, i \in I} [/math]

Но вектора пока не известны, их нужно получить. Имеются оценки пользователей, при помощи которых можно можно найти оптимальные параметры, при которых модель предскажет оценки наилучших образом:

[math] E_{(u,i)}(\hat{r}_{ui}(\Theta) - r_{ui})^2 \to min_{\Theta} [/math]

То есть, нужно найти такие параметры [math] \Theta [/math], чтобы квадрат ошибки был наименьшим. Однако ситуация следующая: оптимизация приведет к наименьшим ошибкам в будущем, но как именно оценки будут спрашивать — неизвестно. Следовательно, это нельзя оптимизировать. Однако, так как оценки уже проставленные пользователями известны, постараемся минимизировать ошибку на тех данных, что у нас уже есть. Так же добавим регуляризатор.

[math] \sum_{(u,i) \in D}{(\hat{r}_{ui}(\Theta) - r_{ui})^2} + \lambda \sum_{\theta \in \Theta}{\theta^2} \to min_{\Theta} [/math]

Определение:

Регуляризация (англ. regularization) в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение. Чаще всего эта информация имеет вид штрафа за сложность модели.

Регуляризация заключается в том, что минимизируется не только ошибка, но и некоторая функция параметров (например, норма вектора параметров). Это позволяет ограничить размер параметров в решении, уменьшает степень свободы модели.

Численная оптимизация

Визуализация градиентного спуска.

[math] J(\Theta) = \sum_{(u,i) \in D}{(r^T_u - r_{ui})^2} + \lambda (\sum_u{||p_u||^2} + \sum_i{||q_i||^2}) [/math]

Необходимо оптимизировать данный функционал. Множество параметров: для каждого объекта и пользователя есть свой вектор, который нужно оптимизировать. Дабы найти минимум функции воспользуемся градиентом - вектор из частных производных по каждомц параметру.

[math] \nabla J(\Theta) = (\frac{\partial J}{\partial \theta_1}, \frac{\partial J}{\partial \theta_2},...,\frac{\partial J}{\partial \theta_n})^T [/math]

Можно воспользоваться градиентным бустингом:

[math] \Theta_{t+1} = \Theta_t - \eta \nabla J(\Theta) [/math]

Проблема же заключается в том, что алгоритм работает медленно, а минимумы которые он находит — локальные, а не глобальные.

Измерение качества рекомендаций

Было предложено измерять качество рекомендаций при помощи RMSE:

[math] RMSE = \sqrt{\frac{1}{|D|} \sum_{(u,i) \in D}{(\hat{r}_{ui} - r_{ui})^2}} [/math]

Однако она также обладает недостатками, хоть и является стандартом измерения качества:

• Пользователи с большим разбросом оценок будут влиять на значение метрики больше, чем остальные.
• Ошибка в предсказании высокой оценки имеет такой же вес, что и ошибка в предсказании низкой оценки.
• Есть риск плохого ранжирования при почти идельаной RMSE и наоборот.

Существуют при этом и другие метрики — метрики ранжирования, на основе полноты и точности. Однако они не так популярны и используются значительно реже.

Источники информации

• Как работают рекомендательные системы.
• Рекомендательные системы: идеи, подходы, задачи.
• Анатомия рекомендательных систем.
• Рекомендательные системы: обзор основных постановок и результатов.