Участница:Наталья Юльцова

Преобразование регулярного выражения в ДКА

1) Преобразовать регулярное выражение в ε-НКА. Будем пользоваться следующим правилом: 1. Для регулярного выражения A|B можем построить следующий КА:

2. Для регулярного выражения AB можем построить следующий КА:

3. Для регулярного выражения A* можем построить следующий КА:

2) Преобразовать ε-НКА в НКА (статья : Автоматы с eps-переходами. Eps-замыкание) 3) Преобразовать НКА в ДКА (статья : Построение по НКА эквивалентного ДКА, алгоритм Томпсона) Пример: преобразовать регулярное выражение (0|1)*1(0|1) в ДКА. 1) Преобразуем регулярное выражение (0|1)*1(0|1) в ε-НКА. Построим сначала автомат для 0|1. Для этого воспользуемся правилом 1.

Далее принимаем (0|1) за А и строим по правилу 3 выражение (0|1)*. После по правилу 2 соединим (0|1)*, 1, и (0|1).

2) Удалим ε-переходы, получим НКА:

3) Преобразуем НКА в ДКА и минимизируем ДКА:

Преобразование ДКА в регулярное выражение с помощью алгебраического метода Бжозовского.

Создадим систему регулярных выражений для каждого состояния в ДКА, а затем решим систему для регулярных выражений [math]R_i[/math], связанных с терминальным состояниями [math]q_i[/math]. Строим уравнения следующим образом: для каждого состояния [math]q_i[/math] уравнение [math]R_i[/math] является объединением переходов, ведущих в это состояние. Переход a из [math]q_i[/math] в [math]q_j[/math] обозначим за [math]aR_i[/math]. Если [math]q_i[/math] - терминальное состояние, то добавим в [math]R_i[/math] [math]\ne \varepsilon[/math]. Это приводит к системе уравнений вида:

[math] \begin{cases} R_1 = a_1*R_1 + a_2*R_2 + a_3*R_3 + ... \\ R_2 = a_1*R_1 + a_2*R_2 + a_3*R_3 + ... + \varepsilon \\ ... \\ R_m = a_1*R_1 + a_2*R_2 + a_3*R_3 + ... + \varepsilon \end{cases} [/math]

где [math]a_x[/math] = ∅ если нет перехода от [math]R_i[/math] к [math]R_j[/math]. Система может быть решена с помощью простой подстановки, за исключением случаев, когда неизвестное появляется как в правой, так и в левой части уравнения. Для этого воспользуемся теоремой Ардена:

Уравнение вида R = Q + RP, где P [math]\ne \varepsilon[/math], имеет решение R = QP*.

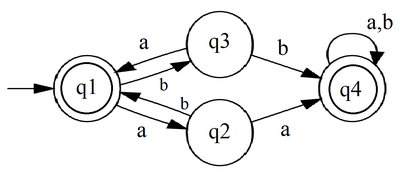
Пример

Найти: Регулярное выражение, удовлетворяющее данному ДКА.

Решение:

[math] \begin{cases} R_1 = b*R_2 + a*R_3 + \varepsilon \\ R_2 = a*R_1 \\ R_3 = b*R_1 \\ R_4 = a*R_2 + b*R_3 + a*R_4 + b*R_4 + \varepsilon \end{cases} [/math]

Рассмотрим первое терминальное состояние:

[math]R_1 = \varepsilon + abR_1 + baR_1 = \varepsilon + R_1(ab+ba)[/math]

Воспользуемся теоремой Ардена:

[math]R_1=(ab+ba)^*[/math]

Рассмотрим второе терминальное состояние :

[math]R_4=R_1(aa+bb)+R_4(a+b)=R_1(aa+bb)(a+b)^*[/math]

Объединим выражения для терминальных состояний и получим искомое регулярное выражение:

[math]R = R_1 + R_4= (ab+ba)^* (\varepsilon + (aa+bb) (a+b)^*)[/math]