Теорема Ладнера — различия между версиями
Assaron (обсуждение | вклад) м (→Описание способа построения A) |
Assaron (обсуждение | вклад) м |
||
| Строка 1: | Строка 1: | ||
'''Теорема Ладнера''' (Ladner's Theorem) утверждает, | '''Теорема Ладнера''' (Ladner's Theorem) утверждает, | ||
что если [[Класс P|P]] не совпадает с [[Класс NP|NP]], то существует язык <tex>L</tex>, | что если [[Класс P|P]] не совпадает с [[Класс NP|NP]], то существует язык <tex>L</tex>, | ||
| − | принадлежащий <tex>NP</tex>, но не являющийся полиномиальным и [[NP-полнота|NP-полным]]. | + | принадлежащий <tex>\mathrm{NP}</tex>, но не являющийся полиномиальным и [[NP-полнота|NP-полным]]. |
==Иллюстрация== | ==Иллюстрация== | ||
| Строка 15: | Строка 15: | ||
Рассмотрим язык [[SAT]] всех удовлетворимых формул. Логично предположить, что как в <tex>A</tex>, | Рассмотрим язык [[SAT]] всех удовлетворимых формул. Логично предположить, что как в <tex>A</tex>, | ||
| − | так и в <tex>\bar{A}</tex> лежит бесконечное множество элементов из <tex>SAT</tex>, | + | так и в <tex>\bar{A}</tex> лежит бесконечное множество элементов из <tex>\mathrm{SAT}</tex>, |
| − | не распознаваемых за полиномиальное время, поэтому <tex>SAT \cap A \not\in P</tex>. | + | не распознаваемых за полиномиальное время, поэтому <tex>\mathrm{SAT} \cap A \not\in \mathrm{P}</tex>. |
| − | Из <tex>A \in P</tex> и <tex>SAT \in NP</tex> следует, что <tex>SAT \cap A \in NP</tex>. | + | Из <tex>A \in \mathrm{P}</tex> и <tex>\mathrm{SAT} \in \mathrm{NP}</tex> следует, что <tex>\mathrm{SAT} \cap A \in \mathrm{NP}</tex>. |
| − | Осталось показать, что <tex>SAT \cap A</tex> не является NP-полным. Пусть | + | Осталось показать, что <tex>\mathrm{SAT} \cap A</tex> не является NP-полным. Пусть |
это не так. Тогда из NP-полноты следует, что существует полиномиальная функция <math>f</math>, | это не так. Тогда из NP-полноты следует, что существует полиномиальная функция <math>f</math>, | ||
| − | [[Сведение по Карпу|сводящая по Карпу]] <tex>SAT</tex> к <tex>SAT \cap A</tex>. | + | [[Сведение по Карпу|сводящая по Карпу]] <tex>\mathrm{SAT}</tex> к <tex>\mathrm{SAT} \cap A</tex>. |
Возьмём формулу <tex>\varphi</tex> длиной <tex>^{2k+1}10</tex>. | Возьмём формулу <tex>\varphi</tex> длиной <tex>^{2k+1}10</tex>. | ||
| − | Она не лежит в <tex>A</tex> и, следовательно, в <tex>SAT \cap A</tex>. | + | Она не лежит в <tex>A</tex> и, следовательно, в <tex>\mathrm{SAT} \cap A</tex>. |
Функция <tex>f</tex> не может перевести <tex>\varphi</tex> в промежуток | Функция <tex>f</tex> не может перевести <tex>\varphi</tex> в промежуток | ||
<tex>\left[^{2k+2}10, ^{2k+4}10\right)</tex> или дальше, так как размер | <tex>\left[^{2k+2}10, ^{2k+4}10\right)</tex> или дальше, так как размер | ||
| Строка 31: | Строка 31: | ||
в этом случае размер выхода экспоненциально меньше длины входа. Добавляя | в этом случае размер выхода экспоненциально меньше длины входа. Добавляя | ||
к этому то, что проверку на принадлежность <tex>f(\varphi)</tex> к | к этому то, что проверку на принадлежность <tex>f(\varphi)</tex> к | ||
| − | <tex>SAT \cap A</tex> можно осуществить за <tex>O(2^{poly})</tex> | + | <tex>\mathrm{SAT} \cap A</tex> можно осуществить за <tex>O(2^{poly})</tex> |
| − | (это следует из её принадлежности классу <tex>NP</tex>), получаем программу, | + | (это следует из её принадлежности классу <tex>\mathrm{NP}</tex>), получаем программу, |
разрешающую <tex>\varphi</tex> за полином. Утверждение о том, что все формулы | разрешающую <tex>\varphi</tex> за полином. Утверждение о том, что все формулы | ||
<tex>\varphi</tex> длиной <tex>^{2k+1}10</tex> принадлежат классу | <tex>\varphi</tex> длиной <tex>^{2k+1}10</tex> принадлежат классу | ||
| − | <tex>P</tex>, скорее всего не верно, и, следовательно, язык | + | <tex>\mathrm{P}</tex>, скорее всего не верно, и, следовательно, язык |
| − | <tex>SAT \cap A</tex> не является NP-полным. | + | <tex>\mathrm{SAT} \cap A</tex> не является NP-полным. |
Заметим, что это объяснение не является доказательством! | Заметим, что это объяснение не является доказательством! | ||
| Строка 42: | Строка 42: | ||
==Доказательство== | ==Доказательство== | ||
Будем искать язык <tex>A</tex>, удовлетворяющий следующим условиям: | Будем искать язык <tex>A</tex>, удовлетворяющий следующим условиям: | ||
| − | #<tex>A \in P</tex> (что влечёт за собой <tex>SAT \cap A \in NP</tex>); | + | #<tex>A \in \mathrm{P}</tex> (что влечёт за собой <tex>\mathrm{SAT} \cap A \in \mathrm{NP}</tex>); |
| − | #<tex>SAT \cap A \not\in P</tex>; | + | #<tex>\mathrm{SAT} \cap A \not\in \mathrm{P}</tex>; |
| − | #<tex>SAT \not \leqslant SAT \cap A</tex>. | + | #<tex>\mathrm{SAT} \not \leqslant \mathrm{SAT} \cap A</tex>. |
| − | Если такой язык существует, то <tex>L = SAT \cap A</tex> является искомым примером множества | + | Если такой язык существует, то <tex>L = \mathrm{SAT} \cap A</tex> является искомым примером множества |
| − | из <tex>NP \setminus (P \cup NPC)</tex>. | + | из <tex>\mathrm{NP} \setminus (\mathrm{P} \cup \mathrm{NPC})</tex>. |
===Утверждение 1=== | ===Утверждение 1=== | ||
| − | Можно перечислить (возможно, с повторениями) все языки из <tex>P</tex>. | + | Можно перечислить (возможно, с повторениями) все языки из <tex>\mathrm{P}</tex>. |
Действительно, рассмотрим последовательность всех программ, упорядоченных по длине: | Действительно, рассмотрим последовательность всех программ, упорядоченных по длине: | ||
| Строка 56: | Строка 56: | ||
Обозначим за <tex>p_i</tex> программу, запускающую <tex>\tilde{p_i}</tex> | Обозначим за <tex>p_i</tex> программу, запускающую <tex>\tilde{p_i}</tex> | ||
с таймером <tex>in^i</tex>. Тогда среди <tex>{p_i}</tex> встречаются | с таймером <tex>in^i</tex>. Тогда среди <tex>{p_i}</tex> встречаются | ||
| − | только программы из <tex>P</tex>, и для каждой полиномиальной программы | + | только программы из <tex>\mathrm{P}</tex>, и для каждой полиномиальной программы |
<tex>\tilde{p_i}</tex>, работающей за полином <tex>g_i(n)</tex>, существует | <tex>\tilde{p_i}</tex>, работающей за полином <tex>g_i(n)</tex>, существует | ||
номер <tex>j</tex> такой, что <tex>jn^j > g_i(n)</tex> для всех натуральных <tex>n</tex> | номер <tex>j</tex> такой, что <tex>jn^j > g_i(n)</tex> для всех натуральных <tex>n</tex> | ||
| Строка 63: | Строка 63: | ||
===Утверждение 2=== | ===Утверждение 2=== | ||
| − | Можно перечислить все функции из <tex>\tilde{P}</tex>. | + | Можно перечислить все функции из <tex>\tilde{\mathrm{P}}</tex>. |
Аналогично предыдущему доказательству, сначала построим последовательность <tex>\tilde{f_i}</tex>, а затем, добавив таймер <tex>in^i</tex>, получим последовательность <tex>f_i</tex>. | Аналогично предыдущему доказательству, сначала построим последовательность <tex>\tilde{f_i}</tex>, а затем, добавив таймер <tex>in^i</tex>, получим последовательность <tex>f_i</tex>. | ||
| Строка 71: | Строка 71: | ||
<tex>A_i</tex> так, что: | <tex>A_i</tex> так, что: | ||
*<tex>\forall i<j, \forall \alpha \in A_i, \beta \in A_j: |\alpha| < |\beta|</tex> (то есть разбиение происходит по длинам, причем <tex>A_i</tex> идут «подряд»), | *<tex>\forall i<j, \forall \alpha \in A_i, \beta \in A_j: |\alpha| < |\beta|</tex> (то есть разбиение происходит по длинам, причем <tex>A_i</tex> идут «подряд»), | ||
| − | *<tex>SAT \cap \bigcup_{i=0}^{k} A_{2i}</tex> отличается от <tex>L(p_k)</tex> элементом <tex>x_{2k}</tex> из <tex>\bigcup_{i=0}^{2k} A_i</tex>, | + | *<tex>\mathrm{SAT} \cap \bigcup_{i=0}^{k} A_{2i}</tex> отличается от <tex>L(p_k)</tex> элементом <tex>x_{2k}</tex> из <tex>\bigcup_{i=0}^{2k} A_i</tex>, |
| − | *для любого <tex>k</tex> существует <tex>x_{2k+1} \in \bigcup_{i=0}^{2k+1} A_i</tex>, для которого выполняются условия <tex>f_k(x_{2k+1}) \in \bigcup_{i=0}^{2k+1} A_i</tex> и <tex>[x_{2k+1} \in SAT] \ne [f_k(x_{2k+1}) \in SAT \cap \bigcup_{i=0}^{k} A_{2i}]</tex>. | + | *для любого <tex>k</tex> существует <tex>x_{2k+1} \in \bigcup_{i=0}^{2k+1} A_i</tex>, для которого выполняются условия <tex>f_k(x_{2k+1}) \in \bigcup_{i=0}^{2k+1} A_i</tex> и <tex>[x_{2k+1} \in \mathrm{SAT}] \ne [f_k(x_{2k+1}) \in \mathrm{SAT} \cap \bigcup_{i=0}^{k} A_{2i}]</tex>. |
[[File:Ladner.png]] | [[File:Ladner.png]] | ||
| − | Если мы сможем построить такие <tex>A_i</tex>, то язык <tex>L = SAT \cap \bigcup_{i=0}^{\infty} A_{2i}</tex> | + | Если мы сможем построить такие <tex>A_i</tex>, то язык <tex>L = \mathrm{SAT} \cap \bigcup_{i=0}^{\infty} A_{2i}</tex> |
будет отличаться от любого полиномиального языка, и ни одна полиномиальная функция не будет сводить | будет отличаться от любого полиномиального языка, и ни одна полиномиальная функция не будет сводить | ||
| − | <tex>SAT</tex> к <tex>L</tex>. | + | <tex>\mathrm{SAT}</tex> к <tex>L</tex>. |
Попытаемся построить такую полиномиальную функцию <tex>f</tex>, что | Попытаемся построить такую полиномиальную функцию <tex>f</tex>, что | ||
<tex>A_i = \left\{x \mid f(|x|) = i\right\}</tex>. Тогда | <tex>A_i = \left\{x \mid f(|x|) = i\right\}</tex>. Тогда | ||
<tex>A=\left\{x \mid f(|x|) \equiv 0 (\mathrm{mod}\ 2) \right\}</tex> и | <tex>A=\left\{x \mid f(|x|) \equiv 0 (\mathrm{mod}\ 2) \right\}</tex> и | ||
| − | <tex>L=SAT \cap A = \left\{\varphi \mid \varphi \in SAT \land f(|\varphi|) \equiv 0 (\mathrm{mod}\ 2) \right\}</tex> | + | <tex>L=\mathrm{SAT} \cap A = \left\{\varphi \mid \varphi \in \mathrm{SAT} \land f(|\varphi|) \equiv 0 (\mathrm{mod}\ 2) \right\}</tex> |
===Построение <tex>f</tex>=== | ===Построение <tex>f</tex>=== | ||
| Строка 92: | Строка 92: | ||
*:если существует <tex>x</tex> такой, что <tex>|x| < \log_2 n</tex> и <tex>p_i(x) \ne [x \in L]</tex>, то <tex>f(n) = f(n-1)+1</tex>, иначе <tex>f(n) = f(n-1)</tex>; | *:если существует <tex>x</tex> такой, что <tex>|x| < \log_2 n</tex> и <tex>p_i(x) \ne [x \in L]</tex>, то <tex>f(n) = f(n-1)+1</tex>, иначе <tex>f(n) = f(n-1)</tex>; | ||
*<tex>f(n-1)=2i+1</tex>: | *<tex>f(n-1)=2i+1</tex>: | ||
| − | *:если существует <tex>x</tex> такой, что <tex>|x| < \log_2 n</tex>,<tex>|f_i(x)| < \log_2 n</tex> и <tex>[x \in SAT] \ne [f_i(x) \in L]</tex>, то <tex>f(n) = f(n-1)+1</tex>, иначе <tex>f(n) = f(n-1)</tex>. | + | *:если существует <tex>x</tex> такой, что <tex>|x| < \log_2 n</tex>,<tex>|f_i(x)| < \log_2 n</tex> и <tex>[x \in \mathrm{SAT}] \ne [f_i(x) \in L]</tex>, то <tex>f(n) = f(n-1)+1</tex>, иначе <tex>f(n) = f(n-1)</tex>. |
Заметим, что вызовы <tex>[\alpha \in L]</tex> делаются для <tex>\alpha</tex>, для которых <tex>f</tex> уже построена. | Заметим, что вызовы <tex>[\alpha \in L]</tex> делаются для <tex>\alpha</tex>, для которых <tex>f</tex> уже построена. | ||
| Строка 101: | Строка 101: | ||
===Полиномиальность <tex>f</tex>=== | ===Полиномиальность <tex>f</tex>=== | ||
| − | Покажем, что <tex>f \in \tilde{P}</tex>. Для упрощения будем считать, что алфавит <tex>\Sigma=\{0,1\}</tex>. | + | Покажем, что <tex>f \in \tilde{\mathrm{P}}</tex>. Для упрощения будем считать, что алфавит <tex>\Sigma=\{0,1\}</tex>. |
<tex>T(n) = T(n-1) + a(n)(b_1(n) + b_2(n) + b_3(n) + b_4(n)) + c_1(n) + c_2(n)</tex>, где: | <tex>T(n) = T(n-1) + a(n)(b_1(n) + b_2(n) + b_3(n) + b_4(n)) + c_1(n) + c_2(n)</tex>, где: | ||
| Строка 107: | Строка 107: | ||
*<tex>a(n)</tex> — время перебора всех слов <tex>x</tex> таких, что <tex>|x| < \log_2 n</tex>; | *<tex>a(n)</tex> — время перебора всех слов <tex>x</tex> таких, что <tex>|x| < \log_2 n</tex>; | ||
*<tex>b_1(n)</tex> — время работы <tex>p_i(x)</tex>; | *<tex>b_1(n)</tex> — время работы <tex>p_i(x)</tex>; | ||
| − | *<tex>b_2(n)</tex> — время работы <tex>[x \in SAT]</tex>; | + | *<tex>b_2(n)</tex> — время работы <tex>[x \in \mathrm{SAT}]</tex>; |
*<tex>b_3(n)</tex> — время работы <tex>[x \in L]</tex>; | *<tex>b_3(n)</tex> — время работы <tex>[x \in L]</tex>; | ||
*<tex>b_4(n)</tex> — время работы <tex>[f_i(x) \in L]</tex>; | *<tex>b_4(n)</tex> — время работы <tex>[f_i(x) \in L]</tex>; | ||
| Строка 131: | Строка 131: | ||
Получаем, что <tex>T(n) = T(n-1) + poly</tex>. Значит, <tex>T(n) \le n \cdot poly </tex>. | Получаем, что <tex>T(n) = T(n-1) + poly</tex>. Значит, <tex>T(n) \le n \cdot poly </tex>. | ||
| − | Поэтому <tex>T(n) \in \tilde{P}</tex> и <tex>A \in P</tex>. | + | Поэтому <tex>T(n) \in \tilde{\mathrm{P}}</tex> и <tex>A \in \mathrm{P}</tex>. |
| − | Таким образом, <tex>f</tex> полиномиальна и <tex>A \in P</tex>. | + | Таким образом, <tex>f</tex> полиномиальна и <tex>A \in \mathrm{P}</tex>. |
===Доказательство выполнения свойств <tex>A</tex>=== | ===Доказательство выполнения свойств <tex>A</tex>=== | ||
Предположим, что <tex>\lim_{n \to \infty}f(n) = 2i</tex>. Это значит, что фунция «застряла» в ветке «иначе» случая два, | Предположим, что <tex>\lim_{n \to \infty}f(n) = 2i</tex>. Это значит, что фунция «застряла» в ветке «иначе» случая два, | ||
| − | но из этого следует, что <tex>SAT</tex> не отличается от <tex>L(p_i)</tex>. Это | + | но из этого следует, что <tex>\mathrm{SAT}</tex> не отличается от <tex>L(p_i)</tex>. Это |
| − | влечёт за собой принадлежность <tex>SAT</tex> к <tex>P</tex>, что противоречит предположению <tex>P \ne NP</tex>. | + | влечёт за собой принадлежность <tex>\mathrm{SAT}</tex> к <tex>\mathrm{P}</tex>, что противоречит предположению <tex>\mathrm{P} \ne \mathrm{NP}</tex>. |
Аналогично, в случае, если <tex>\lim_{n \to \infty}f(n) = 2i+1</tex>. Тогда функция «застряла» в ветке «иначе» случая три. | Аналогично, в случае, если <tex>\lim_{n \to \infty}f(n) = 2i+1</tex>. Тогда функция «застряла» в ветке «иначе» случая три. | ||
| − | Следствием этого является то, что <tex>SAT</tex> функцией <tex>p_i</tex> сводится к конечному множеству, что тоже | + | Следствием этого является то, что <tex>\mathrm{SAT}</tex> функцией <tex>p_i</tex> сводится к конечному множеству, что тоже |
| − | противоречит предположению <tex>P \ne NP</tex>. | + | противоречит предположению <tex>\mathrm{P} \ne \mathrm{NP}</tex>. |
Получается, что <tex>\lim_{n \to \infty}f(n) = +\infty</tex>, но по построению если <tex>f</tex> неограниченно растет, | Получается, что <tex>\lim_{n \to \infty}f(n) = +\infty</tex>, но по построению если <tex>f</tex> неограниченно растет, | ||
то <tex>L</tex> не совпадает ни с каким языком <tex>L(p_i)</tex> и ни одна функция <tex>f_i</tex> не сводит | то <tex>L</tex> не совпадает ни с каким языком <tex>L(p_i)</tex> и ни одна функция <tex>f_i</tex> не сводит | ||
| − | <tex>SAT</tex> к <tex>L</tex>. Следовательно, выполняются все три требуемых свойста, и <tex>L</tex> является примером | + | <tex>\mathrm{SAT}</tex> к <tex>L</tex>. Следовательно, выполняются все три требуемых свойста, и <tex>L</tex> является примером |
| − | языка из <tex>NP\setminus(P \cup NPC)</tex>. | + | языка из <tex>\mathrm{NP}\setminus(\mathrm{P} \cup \mathrm{NPC})</tex>. |
Теорема доказана. | Теорема доказана. | ||
Версия 22:04, 14 апреля 2010
Теорема Ладнера (Ladner's Theorem) утверждает, что если P не совпадает с NP, то существует язык , принадлежащий , но не являющийся полиномиальным и NP-полным.
Содержание
Иллюстрация
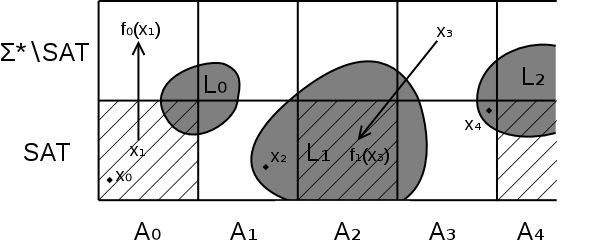
Определим язык как множество таких формул , что чётно. Иными словами, — это язык формул с длинами, лежащими в промежутках Далее будем обозначать как .
Рассмотрим язык SAT всех удовлетворимых формул. Логично предположить, что как в , так и в лежит бесконечное множество элементов из , не распознаваемых за полиномиальное время, поэтому . Из и следует, что .
Осталось показать, что не является NP-полным. Пусть это не так. Тогда из NP-полноты следует, что существует полиномиальная функция , сводящая по Карпу к .
Возьмём формулу длиной . Она не лежит в и, следовательно, в . Функция не может перевести в промежуток или дальше, так как размер выхода полиномиальной функции не может быть экспоненциально больше длины входа. Значит, отображается в меньший промежуток, но в этом случае размер выхода экспоненциально меньше длины входа. Добавляя к этому то, что проверку на принадлежность к можно осуществить за (это следует из её принадлежности классу ), получаем программу, разрешающую за полином. Утверждение о том, что все формулы длиной принадлежат классу , скорее всего не верно, и, следовательно, язык не является NP-полным.
Заметим, что это объяснение не является доказательством!
Доказательство
Будем искать язык , удовлетворяющий следующим условиям:
- (что влечёт за собой );
- ;
- .
Если такой язык существует, то является искомым примером множества из .
Утверждение 1
Можно перечислить (возможно, с повторениями) все языки из .
Действительно, рассмотрим последовательность всех программ, упорядоченных по длине: Обозначим за программу, запускающую с таймером . Тогда среди встречаются только программы из , и для каждой полиномиальной программы , работающей за полином , существует номер такой, что для всех натуральных и делает то же самое, что и . Таким образом, распознает тот же язык, что и .
Утверждение 2
Можно перечислить все функции из .
Аналогично предыдущему доказательству, сначала построим последовательность , а затем, добавив таймер , получим последовательность .
Описание способа построения
Упорядочим все слова по возрастанию длины. Разобьем всё на множества так, что:
- (то есть разбиение происходит по длинам, причем идут «подряд»),
- отличается от элементом из ,
- для любого существует , для которого выполняются условия и .
Если мы сможем построить такие , то язык будет отличаться от любого полиномиального языка, и ни одна полиномиальная функция не будет сводить к .
Попытаемся построить такую полиномиальную функцию , что . Тогда и
Построение
Зададим . Затем рекурсивно определим . Для этого рассмотрим три случая:
- :
- ;
- :
- если существует такой, что и , то , иначе ;
- :
- если существует такой, что , и , то , иначе .
Заметим, что вызовы делаются для , для которых уже построена.
Первый случай позволяет сказать, что ограничена . Второй «ответственен» за множества для чётных , третий — для нечетных. Логарифм в условии необходим для полиномиальности .
Полиномиальность
Покажем, что . Для упрощения будем считать, что алфавит .
, где:
- идёт на вычисление ;
- — время перебора всех слов таких, что ;
- — время работы ;
- — время работы ;
- — время работы ;
- — время работы ;
- — время, необходимое для построения программы ;
- — время, необходимое для построения функции .
, таким образом .
Чтобы построить программу достаточно построить . Из того, что все упорядочены по длине, следует, что длина не превосходит (константа зависит от языка описания программы). Поэтому для построения i-ой программы достаточно перебрать все слов с длиной не больше и вывести i-ое, являющееся программой. Такой способ требует времени. Аналогично можно построить и . Из этого следует, что и тоже полиномиальны.
Получаем, что . Значит, . Поэтому и .
Таким образом, полиномиальна и .
Доказательство выполнения свойств
Предположим, что . Это значит, что фунция «застряла» в ветке «иначе» случая два, но из этого следует, что не отличается от . Это влечёт за собой принадлежность к , что противоречит предположению .
Аналогично, в случае, если . Тогда функция «застряла» в ветке «иначе» случая три. Следствием этого является то, что функцией сводится к конечному множеству, что тоже противоречит предположению .
Получается, что , но по построению если неограниченно растет, то не совпадает ни с каким языком и ни одна функция не сводит к . Следовательно, выполняются все три требуемых свойста, и является примером языка из .
Теорема доказана.