Карта глубины — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Построение с помощью свёрточных нейронных сетей)
(Метки: правка с мобильного устройства, правка из мобильной версии)
(→‎Построение с помощью свёрточных нейронных сетей)
(Метки: правка с мобильного устройства, правка из мобильной версии)
Строка 51: Строка 51:
 
* "Ищем реальную карту глубины для обучения": с помощью карты смещений, можем построить карту глубины <math>y</math> вышеописанным способом. Также допустимы другие способы построения карты глубины для обучения нейронной сети.
 
* "Ищем реальную карту глубины для обучения": с помощью карты смещений, можем построить карту глубины <math>y</math> вышеописанным способом. Также допустимы другие способы построения карты глубины для обучения нейронной сети.
  
−
*  '''Функция потерь''': определим [[Функция потерь и эмпирический риск|функцию потерь]], для предсказанной карты <math>\hat y</math>, <math>d_i = log( y_i) - log (\hat y_i)</math>, <math>\lambda \in [0, 1]</math> и <math>n </math> - количество пикселей.
+
*  '''Функция потерь''': определим [[Функция потерь и эмпирический риск|функцию потерь]], для предсказанной карты <math>\hat y</math>, <math>d_i = log( y_i) - log (\hat y_i)</math>, <math>\lambda \in [0, 1]</math> и <math>n </math> - количество пикселей.<math>L(y, \hat y) =  \frac{1}{n} \sum\limits_{i} d^2_i - \frac{\lambda}{n^2}(\sum\limits_{i} d_i)^2</math>, где <math>y_i</math> и <math>\hat y_i</math> это i пискель для для реальной карты глубин и для предсказанной карты, соответственно. Гиперпараметр <math>\lambda</math>, нужен для того, чтобы функция потерь меньше росла при большом количестве пикселей, предсказание для которых достаточно близко к реальному. Например, если <math>\lambda = 0</math>, то мы просто придём к оптимизации в L2 для <math>d_i</math>, т.е. <math>L(y, \hat y) =  \frac{1}{n} \sum\limits_{i} d^2_i </math>.<ref name="loss">David Eigen, Christian Puhrsch, Rob Fergus "Depth Map Prediction from a Single Imageusing a Multi-Scale Deep Network" стр. 5</ref>  
−
<math>L(y, \hat y) =  \frac{1}{n} \sum\limits_{i} d^2_i - \frac{\lambda}{n^2}(\sum\limits_{i} d_i)^2</math>,
 
−
где <math>y_i</math> и <math>\hat y_i</math> это i пискель для для реальной карты глубин и для предсказанной карты, соответственно. Гиперпараметр <math>\lambda</math>, нужен для того, чтобы функция потерь меньше росла при большом количестве пикселей, предсказание для которых достаточно близко к реальному. Например, если <math>\lambda = 0</math>, то мы просто придём к оптимизации в L2 для <math>d_i</math>, т.е. <math>L(y, \hat y) =  \frac{1}{n} \sum\limits_{i} d^2_i </math>.<ref name="loss">David Eigen, Christian Puhrsch, Rob Fergus "Depth Map Prediction from a Single Imageusing a Multi-Scale Deep Network" стр. 5</ref>  
 
  
 
* '''Обучение свёрточной нейронной сети''': далее идёт обычное обучение нейронной сети по карте различий путем обратного распространения ошибки, оптимизируя заданную выше функцию потерь.
 
* '''Обучение свёрточной нейронной сети''': далее идёт обычное обучение нейронной сети по карте различий путем обратного распространения ошибки, оптимизируя заданную выше функцию потерь.

Версия 21:25, 20 января 2021

Карта глубины (англ. depth map) — это изображение, на котором для каждого пикселя вместо цвета хранится его расстояние до камеры.[1]

В компьютерной 3D-графике и компьютерном зрении карта глубины представляет собой изображение или канал изображения, содержащий информацию о расстоянии поверхностей объектов сцены от точки обзора.

Мотивация

Карта глубины изображения содержит в себе информацию о расстоянии между различными объектами или частями объектов, представленных на данном изображении. Эта информация может быть полезна во многих областях.

  • Для создания 3D-сенсеров. Они способны строить трёхмерную картину своего окружения, используются для ориентации автономного робота в пространстве.
  • Для систем, использующих технологии дополненной и виртуальной реальности. Например, камеры, которые фиксируют действия пользователя при игре в видеоигру, использующую технологию виртуальной реальности.
  • Нельзя не отметить, беспилотные автомобили, которые так же используют карты глубин для ориентации на дороге.
  • Для обработки фотографий. Например, карты глубин используют для размытия фона на фотографии, чтобы добиться более чёткого выделения на ней человека[2].

Методы построения карты глубины

Карта глубины может быть получена с помощью специальной камеры глубины, по стереопаре изображений, а также с помощью нейронных сетей.

Построение с помощью специальных камер глубин

Рисунок 1. Пример работы ToF-камеры.
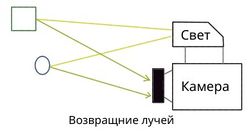
  • ToF-камеры (англ. Time of Flight). Данный метод основан на измерении задержки света. Фактически нам нужно измерить задержку, с которой свет возвращается в каждую точку. Либо, если у нас несколько сенсоров с разным временем накопления заряда, то, зная сдвиг по времени относительно источника для каждого сенсора и снятой яркости вспышки, мы можем рассчитать сдвиг и, соответственно, расстояние до объекта, причем увеличивая количество сенсоров — увеличиваем точность.
  • Структурированные световые камеры (aнгл. Structured light camera). Это один из самых старых и дешёвых способов построить карту глубин. Основная идея крайне проста. Ставим рядом проектор, который создает, например, горизонтальные (а потом вертикальные) полоски и рядом камеру, которая снимает картину с полосками. В некоторых вариантах используются псевдослучайный набор точек (MS Kinect — бесконтактный сенсорный игровой контроллер, для консолей Xbox 360, Xbox One и персональных компьютеров под управлением ОС Windows[3].). Проекторы обычно работают в инфракрасном спектре, очевидно, чтобы не мешать пользователям. Поскольку камера и проектор смещены друг относительно друга, то и полоски также будут смещаться пропорционально расстоянию до объекта. Измеряя это смещение, мы можем рассчитывать расстояние до объекта. Вполне понятны проблемы, с которыми можно столкнуться при использовании этого метода: это необходимость настройки и калибровки проектора, и проблема того, что нам нужно относительно благоприятное освещение. К примеру, солнце может засветить полосы, и что-то распознать будет тяжело.

Построения карты глубины по стереопаре

Идея, лежащая в основе построения карты глубины по стереопаре, очень проста. Для каждой точки на одном изображении выполняется поиск парной ей точки на другом изображении. А по паре соответствующих точек можно выполнить триангуляцию и определить координаты их прообраза в трехмерном пространстве. Зная трехмерные координаты прообраза, глубина вычисляется как расстояние до плоскости камеры.

Парную точку нужно искать на эпиполярной[4] линии. Соответственно, для упрощения поиска изображения выравнивают так, чтобы все эпиполярные линии были параллельны сторонам изображения (обычно горизонтальны). Более того, изображения выравнивают так, чтобы для точки с координатами [math](x_0, y_0)[/math] соответствующая ей эпиполярная линия задавалась уравнением [math]x = x_0[/math]. Тогда для каждой точки, соответствующую ей парную точку, нужно искать в той-же строчке на изображении со второй камеры. Такой процесс выравнивания изображений называют ректификацией (rectification).

Рисунок 2. Результат построения карты смещений по 2 картинкам.[5]

После того, как изображения ректифицированы, выполняют поиск соответствующих пар точек. Для каждого пикселя одной картинки с координатами [math](x_0, y_0)[/math] выполняется поиск пикселя на другой картинке. При этом предполагается, что пиксель на второй картинке должен иметь координаты [math](x_0 - d, y_0)[/math], где d — величина называемая смещением. Поиск соответствующего пикселя выполняется путем вычисления максимума функции отклика, в качестве которой может выступать, например, корреляция окрестностей пикселей. В результате получается карта смещений, пример которой приведен на рис. 2.

Собственно значения глубины обратно пропорциональны величине смещения пикселей.

Использование нейронных сетей

Существует множество решений данной проблемы, использующих нейронные сети. Приведём пару примеров таких решений.

Построение с помощью свёрточных нейронных сетей

Используем сверточные нейронные сети для построения карты глубины следующим образом:

  • Создаем карту смещений: используя 2 изображения с камер, близко расположенных друг к другу, создаем карту различий, точно так же как в методе построения по стереопаре.
  • "Ищем реальную карту глубины для обучения": с помощью карты смещений, можем построить карту глубины [math]y[/math] вышеописанным способом. Также допустимы другие способы построения карты глубины для обучения нейронной сети.
  • Функция потерь: определим функцию потерь, для предсказанной карты [math]\hat y[/math], [math]d_i = log( y_i) - log (\hat y_i)[/math], [math]\lambda \in [0, 1][/math] и [math]n [/math] - количество пикселей.[math]L(y, \hat y) = \frac{1}{n} \sum\limits_{i} d^2_i - \frac{\lambda}{n^2}(\sum\limits_{i} d_i)^2[/math], где [math]y_i[/math] и [math]\hat y_i[/math] это i пискель для для реальной карты глубин и для предсказанной карты, соответственно. Гиперпараметр [math]\lambda[/math], нужен для того, чтобы функция потерь меньше росла при большом количестве пикселей, предсказание для которых достаточно близко к реальному. Например, если [math]\lambda = 0[/math], то мы просто придём к оптимизации в L2 для [math]d_i[/math], т.е. [math]L(y, \hat y) = \frac{1}{n} \sum\limits_{i} d^2_i [/math].[6]
  • Обучение свёрточной нейронной сети: далее идёт обычное обучение нейронной сети по карте различий путем обратного распространения ошибки, оптимизируя заданную выше функцию потерь.

В итоге, по обученной нейронной сети мы можем создавать карту глубины, не проводя расчётов для поиска карт смещения и имея только изображение объекта или пространства. [7]

Также возможно использование усложнённых архитектур свёрточных нейронных сетей типа DenseNet.

DenseNet[8] — это свёрточная нейронные сеть, в которой выход каждого из слоев подаётся на вход всем слоям, лежащих ниже.

Построение с помощью капсульных нейронных сетей

Свёрточные нейронные сети способны регистрировать только наличие какого-либо объекта на картинке, не кодируя его ориентацию и положение. Но капсульные нейронные сети (англ. Capsule Neural Network) лишены этого недостатка.

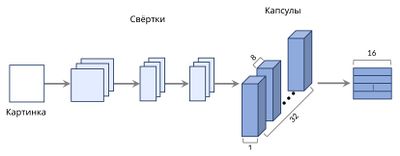
Рисунок 3. Структура капсульной нейронной сети [9].

"Капсульная нейронная сеть" состоит из капсул или групп нейронов, чтобы идентифицировать закономерности в изображении. Эта информация поступает в виде векторов, содержащих ориентацию и положение узоров на изображении, которое затем принимается капсулами более высокого уровня. Капсулы более высокого уровня обрабатывают эту информацию из нескольких капсул более низкого уровня и впоследствии выдают прогноз. Капсулы одного уровня не имеют связей друг с другом и вычисляют информацию независимо друг от друга. Капсулы образуются путем разделения выходных данных из свёрточного слоя. Мы делим наш трехмерный вектор на капсулы методом "нарезания" таким образом, чтобы в каждой капсуле была информация о каждом пикселе, т.е. по трехмерной координате.

Состояние нейронов капсульной нейронной сети внутри изображения фиксирует свойство области или объекта внутри изображения: его положение и ориентацию.

Использование капсульной нейронной сети аналогично с использованию обычных свёрточных сетей, описанному выше. В целом, данная сеть показывает более точные результаты предсказания глубины.

См. также

Примечания

  1. ↑ Alexey Kurakin "Основы стереозрения"[1]
  2. ↑ Примеры из "Research Guide for Depth Estimation with Deep Learning"[2]
  3. ↑ О MicriSoft Kinect [3]
  4. ↑ Информация о эпиполярной геометрии[4]
  5. ↑ "Основы стереозрения" Рис. 3 [5]
  6. ↑ David Eigen, Christian Puhrsch, Rob Fergus "Depth Map Prediction from a Single Imageusing a Multi-Scale Deep Network" стр. 5
  7. ↑ Реализация, основанная на свёрточных нейронных сетях [6]
  8. ↑ Оригинальная статья описывающая DenseNet [7]
  9. ↑ "Design and Investigation of Capsule Networks for Sentence Classification" Figure 2. [8]

Источники информации

  • Р.А. Чугунов, А.Д. Кульневич, С.В. Аксенов "Методика построения карт глубины стереоизображения с помощью капсульной нейронной сети" [9]
  • Alexey Kurakin "Основы стереозрения" [10]
  • Dmitriy Vatolin "Камеры глубины — тихая революция" [11]
  • Ibraheem Alhashim, Peter Wonka "High Quality Monocular Depth Estimation via Transfer Learning" [12]
  • David Eigen, Christian Puhrsch, Rob Fergus "Depth Map Prediction from a Single Imageusing a Multi-Scale Deep Network [13]
  • Sunil Prakash, Gaelan Gu "Simultaneous Localization And Mapping with depth Prediction using Capsule Networks for UAVs" [14]
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Карта_глубины&oldid=79320»