Индексация данных. Упорядоченные и хеш-индексы — различия между версиями
(→Ускоряемые запросы) |
(→Упорядоченные индексы) |
||
| Строка 97: | Строка 97: | ||
* Предварительная обработка | * Предварительная обработка | ||
| − | ** Ключи упорядочиваются по возрастанию - так как ключ составной, то используем лексикографисечкое | + | ** Ключи упорядочиваются по возрастанию - так как ключ составной, то используем лексикографисечкое упорядочивание, после упорядочиваем по возрастанию и строим поверх этого дерево поиска |
* Поиск в индексе | * Поиск в индексе | ||
| − | ** | + | ** Ищем данные в дереве поиска. Используемое дерево поиска должно поддерживать операции вставки, удаления и поиска |
Деревья поиска | Деревья поиска | ||
| − | * Количество операций | + | * Количество операций обычно пропорционально $O$(высоты). Так как время выполнение операций зависит от высоты дерева, для оптимизации времени нужно минимизировать высоту |
| − | |||
| − | |||
* Размер узла | * Размер узла | ||
** Хотим эффективно использовать страницы | ** Хотим эффективно использовать страницы | ||
| − | ** | + | ** Используем сильно ветвящиеся деревья. Так размер узла будет примерно равен странице и высота дерева будет минимальной |
=== $B$ и $B+$ деревья === | === $B$ и $B+$ деревья === | ||
| + | |||
| + | Обычно в качестве сильно ветвящихся деревьев поиска берут $B$ и $B+$ деревья и их разновидности. | ||
* $B$ деревья степени $n$ | * $B$ деревья степени $n$ | ||
| − | ** | + | ** В каждом узле от $\frac{n}{2}$ до n детей |
** Указатели и ключи хранятся в узлах | ** Указатели и ключи хранятся в узлах | ||
* $B+$ деревья степени $n$ | * $B+$ деревья степени $n$ | ||
| Строка 119: | Строка 119: | ||
* $B+$ меньше данных в узлах - сильнее ветвятся | * $B+$ меньше данных в узлах - сильнее ветвятся | ||
| − | * $B+$ на одну страницу глубже | + | * $B+$ на одну страницу глубже, а это значит что больше образений к листу. |
| − | Мы храним корень и несколько первых уровней в памяти для быстрого обращения, из-за этого время работы может резко возрастать, когда заканчивается закешированные уровни. | + | Мы храним корень и несколько первых уровней в памяти для быстрого обращения, из-за этого время работы может резко возрастать, когда заканчивается закешированные уровни. Поэтому даже один лишний уровень в дереве может значительно увеличить время исполнения |
=== Плотные и разряженные индексы === | === Плотные и разряженные индексы === | ||
| + | Индексы также делятся на плотные и разряженные | ||
| + | * Плотный индекс. Храним ключи всех элементов подряд | ||
| + | * Разряженные индекс. Храним ключи части элементов | ||
| + | ** Обычно – один на страницу, мы можем найти данные в рамках этой страницы без загрузки новых. Разряженный индекс бычно используется для кластеризованных индексов | ||
| + | ** Уменьшает число уровней так как храним меньше индексов. Вспоминая что даже один уровень может повысить количество загрузок в два раза, понимаем что разряженные индексы могут сильно оптимизировать базу данных | ||
| − | + | Так как упорядоченный индекс хранит сами данные в узлах, а не только хеш, то чем больше индексируеммые данные, тем меньше степень ветвления, тем больше высота дерева. | |
| − | + | Поэтому в упорядоченных индексах, в отличии от хеш-индексов, нужно обращать внимание на то, что является индексом: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Так как | ||
| − | *Строки | + | *Строки - часто бывают большие, нужно очень аккуратно |
| − | ** | + | **Если есть последовательно упорядоченные строки, то можно использовать префиксы, сильно оптимизируя размер индекса |
| − | + | *Суррогатные ключи. Обычно имеют малый размер, поэтому получается низкое и широкое дерево поиска, что нам и нужно | |
| − | + | *Изменяющиеся данные. При изменении данных нужно перестраивать дерево, это не эффективно | |
| − | *Суррогатные ключи | + | **Индексы часто не умеют уменьшаться~--- удаление данных не приводит к уменьшению дерева. Подразумевается, что запускается отдельная программа, которая перестраивает индексы |
| − | |||
| − | |||
| − | |||
| − | *Изменяющиеся данные | ||
| − | ** | ||
| − | |||
| − | |||
| Строка 152: | Строка 143: | ||
* Проверка существования ключа | * Проверка существования ключа | ||
* Поиск по ключу | * Поиск по ключу | ||
| − | * Минимум и максимум среди значений, на которых построен ключ | + | * Минимум и максимум среди значений, на которых построен ключ, в хеш-таблицах этого нет |
| − | * | + | * Можно реализовать поиск в диапазоне |
| − | ** | + | ** В хеш-индексах единственный способ - перебрать всю таблицу, поэтому обчно так не делают. А в упорядоченных нет с этим проблем, если все необходимые столбцы входят в ключ |
| − | ** count. count * работает | + | ** ''count''. count * работает быстрее, так как не нужно идти по всем данным |
| − | * Если построен на строках, like по префиксу | + | * Если построен на строках, ''like'', но только по префиксу |
==Литература== | ==Литература== | ||
Версия 13:12, 27 декабря 2021
Содержание
Индексы
Индексы нужны для того, чтобы оптимально искать нужные записи в таблице.
Всего есть два способа найти нужные данные:
- Полный просмотр таблицы
- Последовательный перебор записей
- Быстро работает на маленьких таблицах, но медленно на средних и больших
- Если выбираем большую часть данных, то работает быстро. Иначе - медленно
- Индекс
- Произвольный набор столбцов
- Требуется предварительная обработка таблицы как при построении, так и при обновлении
- Быстрый поиск в индексе, сразу получаем указатель на запись
На больших данных вся таблица не помещяется в память, из-за этого время работы очень сильно возрастает.
Из-за всего вышеперечисленного, на больших данных использование полного просмотра становится на практике неприемлимым и используется индексация. На маленьких данных полный перебор работает хорошо и создание дополнительных струкрур поверх данных не окупается, поэтому может применяться на практике.
Кластеризованный индекс
Если данные в таблице хранятся в порядке индекса, то такой индекс называется кластеризованным. Кластеризованный индекс позволяет увеличить скорость просмотра, так как нет дополнительной операции загрузки данных, однако так хранить данные возможно только если в таблице есть всего один индекс.
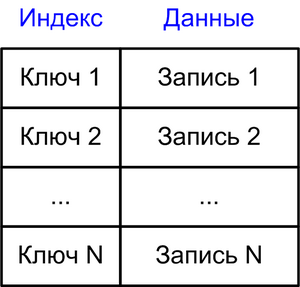
Структура Индекса
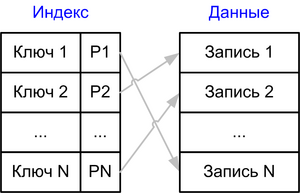
В общем случае индексы хранят отображение из ключей на идентификаторы записей, которые ведут на записи, которые мы загружаем
Есть два подхода к реализации индексов:
- Хеш-таблицы
- Деревья поиска
Хеш-индексы
Хеш-функция задается разработчиком СУБД а не пользователем, чаще всего это эффективно вычисляемые хеш-функции, которые имеют гарантии статистического распределения. Атаки возможны, однако хеш-функцию легко поменять, поэтому атаки ненадежны.
- Предварительная обработка
- Подсчет хешей ключей.
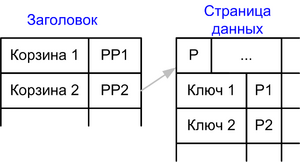
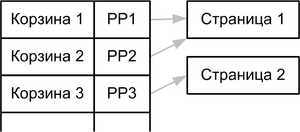
- Разбиение на корзины
- Поиск в индексе
- Просмотр корзины
- Несколько ключей в корзине. Коллизии могут быть, так как индекс не всегда ключ, поэтому нормально если есть повторяющиеся начения. Хеш-таблица все еще честная, но она должна понимать, что значения могут дублироваться.
- Если хеш-индекс является надключем, то СУБД может этим воспользоваться и гарантировать, что дублирующихся значений не будет.
- Заголовок помещяется в памяти
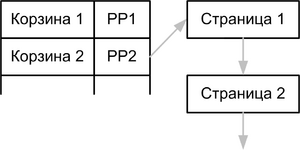
Однако может наступить момент, когда очередная корзина не помещается в страницу, в таком случае мы так же храним их цепочками.
- Так как хеш-функция хорошая, то в цепочке только полезные данные
- Если цепочка длинная, значит этому набору столбцов соответствует много строк, значит база данных так и задумывалась.
При этом получаем линейное время поиска Но в случае если данных много, мы не можем просто увеличить число корзин и перенести данные, так как перехешировать таблицу очень долго
Расширяемое хеширование
Изначально создаем большое количество корзин, сильно больше чем требуется. Пока мало данных Храним несколько корзин на одной странице, чтобы не аллоцировать для каждой корзины по отдельной странице.
- Обычно выбираем набор корзин, которые идут подряд
- При переполнении страницы разделенем корзины на две страницы
- Не работает при плохой хеш-функции, но у нас хорошая
При переполнении страницы мы:
- разделяем ее на несколько страниц
- разделим страницы, которые на нее ссылались, на несколько групп
Стоимость: $1$ чтение и запись стольких страниц, на сколько мы разделили (обычно $2$)
- Каждой такой группе выделим по странице
Побитное расширяемое хеширование
Заранее сделаем заголовок большого размера.
- Глубина хеша $n$ - создаем корзины для $n$ бит нашего хеша
- Получаем $2^n$ корзин
- Для каждой страницы хранится ее локальная глубина $k$, это значит что она хранит $2^{n−k}$ последовательных корзин на странице. При этом локальная глубина может быть разной для разных страниц
- При переполнении происходит разделение корзин. Страница глубины $k$ разделяется на две глубины $k+1$
Есть точные гарантии по производительности~--- все наши затраты измеряются единицами страниц.
Ускоряемые запросы
- Проверка существования ключа
- Проверка повторений (ключи)
- in - только если есть все необходимые атрибуты, то есть даны все столбцы, которые есть в хеш-индексе. Иначе индек не поможет, так как нет способа перебрать все варианты
- exist - только если есть все необходимые атрибуты, анологично с in
- count - при запросе count* зачастую можно посчитать по индексу количество записей с определенным набором стобцов, не обращаясь к самим записям, что дает существенный выигрыш по премени
- Поиск по ключу
- Естественные соединения. Если есть идентификатор, по этому идентификатору есть хеш-индекс, это, в свою очередь, позволяет быстро найти запись.
Упорядоченные индексы
Традиционно реализуются на деревьях поиска
- Предварительная обработка
- Ключи упорядочиваются по возрастанию - так как ключ составной, то используем лексикографисечкое упорядочивание, после упорядочиваем по возрастанию и строим поверх этого дерево поиска
- Поиск в индексе
- Ищем данные в дереве поиска. Используемое дерево поиска должно поддерживать операции вставки, удаления и поиска
Деревья поиска
- Количество операций обычно пропорционально $O$(высоты). Так как время выполнение операций зависит от высоты дерева, для оптимизации времени нужно минимизировать высоту
- Размер узла
- Хотим эффективно использовать страницы
- Используем сильно ветвящиеся деревья. Так размер узла будет примерно равен странице и высота дерева будет минимальной
$B$ и $B+$ деревья
Обычно в качестве сильно ветвящихся деревьев поиска берут $B$ и $B+$ деревья и их разновидности.
- $B$ деревья степени $n$
- В каждом узле от $\frac{n}{2}$ до n детей
- Указатели и ключи хранятся в узлах
- $B+$ деревья степени $n$
- От $\frac{n}{2}$ до $n$ детей
- Указатели хранятся в листьях
- $B+$ меньше данных в узлах - сильнее ветвятся
- $B+$ на одну страницу глубже, а это значит что больше образений к листу.
Мы храним корень и несколько первых уровней в памяти для быстрого обращения, из-за этого время работы может резко возрастать, когда заканчивается закешированные уровни. Поэтому даже один лишний уровень в дереве может значительно увеличить время исполнения
Плотные и разряженные индексы
Индексы также делятся на плотные и разряженные
- Плотный индекс. Храним ключи всех элементов подряд
- Разряженные индекс. Храним ключи части элементов
- Обычно – один на страницу, мы можем найти данные в рамках этой страницы без загрузки новых. Разряженный индекс бычно используется для кластеризованных индексов
- Уменьшает число уровней так как храним меньше индексов. Вспоминая что даже один уровень может повысить количество загрузок в два раза, понимаем что разряженные индексы могут сильно оптимизировать базу данных
Так как упорядоченный индекс хранит сами данные в узлах, а не только хеш, то чем больше индексируеммые данные, тем меньше степень ветвления, тем больше высота дерева. Поэтому в упорядоченных индексах, в отличии от хеш-индексов, нужно обращать внимание на то, что является индексом:
- Строки - часто бывают большие, нужно очень аккуратно
- Если есть последовательно упорядоченные строки, то можно использовать префиксы, сильно оптимизируя размер индекса
- Суррогатные ключи. Обычно имеют малый размер, поэтому получается низкое и широкое дерево поиска, что нам и нужно
- Изменяющиеся данные. При изменении данных нужно перестраивать дерево, это не эффективно
- Индексы часто не умеют уменьшаться~--- удаление данных не приводит к уменьшению дерева. Подразумевается, что запускается отдельная программа, которая перестраивает индексы
Ускоряемые запросы
- Проверка существования ключа
- Поиск по ключу
- Минимум и максимум среди значений, на которых построен ключ, в хеш-таблицах этого нет
- Можно реализовать поиск в диапазоне
- В хеш-индексах единственный способ - перебрать всю таблицу, поэтому обчно так не делают. А в упорядоченных нет с этим проблем, если все необходимые столбцы входят в ключ
- count. count * работает быстрее, так как не нужно идти по всем данным
- Если построен на строках, like, но только по префиксу
Литература
- Дейт К. Введение в системы баз данных (Приложение Г)
- Кнут Д. Искусство программирования. Том 3. Сортировка и поиск
- Silberschatz A., Korth H. F., Sudarshan S. Database System Concepts