Оценка качества в задачах классификации — различия между версиями
(→F₁ score) |
(→change formula for F₁ score) |
||
| Строка 87: | Строка 87: | ||
= F₁ score = | = F₁ score = | ||
Для общей оценки качества классификатора часто используют F₁ меру — среднее гармоническое между precision и recall: | Для общей оценки качества классификатора часто используют F₁ меру — среднее гармоническое между precision и recall: | ||
| − | : <tex>F_1 = \left ( \dfrac{Prec^{-1} + Recall^{-1}}{2} \right )^{-1} = 2 \cdot \dfrac{Prec \cdot Recall}{ | + | : <tex>F_1 = \left ( \dfrac{Prec^{-1} + Recall^{-1}}{2} \right )^{-1} = 2 \cdot \dfrac{Prec \cdot Recall}{Prec + Recall}</tex> |
F₁ мера так же может быть обобщена до F<sub>β</sub>: | F₁ мера так же может быть обобщена до F<sub>β</sub>: | ||
Версия 01:38, 16 марта 2022
Содержание
Общие понятия
- TP — true positive, классификатор верно отнёс объект к рассматриваемому классу.
- TN — true negative, классификатор верно утверждает, что объект не принадлежит к рассматриваемому классу.
- FP — false positive, классификатор неверно отнёс объект к рассматриваемому классу.
- FN — false negative, классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу.
Confusion matrix (матрица несоответствий) наглядно показывает суть этих показателей:
| Принадлежит классу (P) | Не принадлежит классу (N) | |
|---|---|---|
| Предсказана принадлежность классу | TP | FP |
| Предсказано отсутствие принадлежности к классу | FN | TN |
Для многоклассовой классификации матрица несоответствий строится по тому же принципу:
| Предсказанный класс | Класс 1 (C₁) | Класс 2 (C₂) | Класс 3 (C₃) |
|---|---|---|---|
| 1 (P₁) | T₁ | F₁₂ | F₁₃ |
| 2 (P₂) | F₂₁ | T₂ | F₂₃ |
| 3 (P₃) | F₃₁ | F₃₂ | T₃ |
В этом случае TP, TN, FP и FN считаются относительно некоторого класса (i) следующим образом:
Простые оценки
- Accuracy (точность), показывает долю правильных классификаций. Несмотря на очевидность и простоту является одной из самых малоинформативных оценок классификаторов.
- Recall (полнота), так же sensitivity и TPR (true positive rate), показывает долю найденных объектов класса к общему числу объектов класса. Иначе говоря то, насколько хорошо наш классификатор находит объекты из класса.
- Precision (да, тоже точность), показывает долю объектов класса среди объектов выделенных классификатором.
- Specificity, показывает долю верных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор правильно не относит объекты к классу.
- Fall-out, так же FPR (false positive rate), показывает долю неверных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор ошибается при отнесении того или иного объекта к классу.
В виду того, что такие оценки никак не учитывают изначальное распределение классов в выборке (что может существенно влиять на полученное значение), так же существуют взвешенные варианты этих оценок (в терминах многоклассовой классификации):
- Precision
- Recall
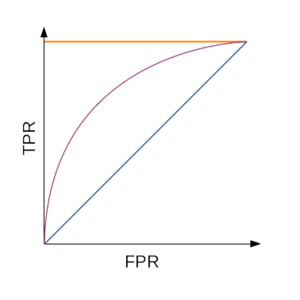
ROC кривая
Для наглядной оценки качества алгоритма применяется ROC кривая. Кривая строится на плоскости, определённой осями полноты (recall, TPR) по вертикали и частоты ложных срабатываний (FPR, 1-Spc).
Чтобы построить кривую:
- Запустить классификатор на тестовой выборке
- Отсортировать результаты по уверенности классификатора в принадлежности объекта к классу
- Пока не кончились элементы:
- Взять объект с максимальной уверенностью
- Сравнить метку с реальной
- Пересчитать TPR и FPR на взятых объектах
- Поставить точку, если обе характеристики не NaN / ±∞
- Построить кривую по точкам
Таким образом число точек не превосходит число объектов, идеальный алгоритм проходит через точку (0;1), худший (например, монетка) — прямая TPR = FPR. Для численной же оценки алгоритма по ROC кривой используется значение площади под ней (AUC, area under curve). Таким образом идеальный алгоритм имеет AUC равный 1, а плохой — 0,5.
F₁ score
Для общей оценки качества классификатора часто используют F₁ меру — среднее гармоническое между precision и recall:
F₁ мера так же может быть обобщена до Fβ:
Fβ измеряет эффективность классификатора учитывая recall в β раз более важным чем precision.
Для многоклассовой классификации с учётом изначального распределения по классам имеет смысл рассматривать микро- и макро- F меру: