Трансформер — различия между версиями
Nilaev (обсуждение | вклад) (Написал статью про трансформеры) |
Nilaev (обсуждение | вклад) (обновление стилей) |
||
| Строка 2: | Строка 2: | ||
==Архитектура трансформера== | ==Архитектура трансформера== | ||
| − | [[Файл:TransformerSimpleArchitecture.png|350px|thumb|right|Архитектура трансформера]] | + | [[Файл:TransformerSimpleArchitecture.png|350px|thumb|right|Архитектура трансформера<ref>https://jalammar.github.io/illustrated-transformer/</ref>]] |
Устройство трансформера состоит из кодирующего и декодирующего компонентов. На вход принимается некая последовательность, создается ее [[:Векторное_представление_слов|векторное представление]] (англ. ''embedding''), векторизованная последовательность поступает в кодирующий компонент, а затем декодирующий компонент получает на вход часть этой последовательности и выход кодирующего. В результате получается новая выходная последовательность. | Устройство трансформера состоит из кодирующего и декодирующего компонентов. На вход принимается некая последовательность, создается ее [[:Векторное_представление_слов|векторное представление]] (англ. ''embedding''), векторизованная последовательность поступает в кодирующий компонент, а затем декодирующий компонент получает на вход часть этой последовательности и выход кодирующего. В результате получается новая выходная последовательность. | ||
| Строка 10: | Строка 10: | ||
==Архитектура трансформера-кодировщика== | ==Архитектура трансформера-кодировщика== | ||
| − | [[Файл:TransformerEncoderArchitecture.png|150px|thumb|left|Архитектура трансформера-кодировщика]] | + | [[Файл:TransformerEncoderArchitecture.png|150px|thumb|left|Архитектура трансформера-кодировщика<ref>https://arxiv.org/abs/1706.03762</ref>]] |
Рассмотрим последовательно шаг за шагом этапы кодировщика: | Рассмотрим последовательно шаг за шагом этапы кодировщика: | ||
| Строка 19: | Строка 19: | ||
3. Полученный вектор <math>h_i</math> подается на вход в блок многомерного самовнимания (англ. ''multi-headed self-attention''). | 3. Полученный вектор <math>h_i</math> подается на вход в блок многомерного самовнимания (англ. ''multi-headed self-attention''). | ||
| − | <math>h^j_i = Attn(W^j_q h_i, W^j_k H, W^j_v H)</math>, где <math>W</math> - обучаемые матрицы, <math>W_q</math> для запроса, <math>W_k</math> для ключа, <math>W_v</math> для значения. Подробное объяснения работы механизма self-attention будет разобрано ниже. | + | <math>h^j_i = \mathrm{Attn}(W^j_q h_i, W^j_k H, W^j_v H)</math>, где <math>W</math> {{---}} обучаемые матрицы, <math>W_q</math> для запроса, <math>W_k</math> для ключа, <math>W_v</math> для значения. Подробное объяснения работы механизма self-attention будет разобрано ниже. |
4. Затем необходима конкатенация, чтобы вернуться в исходную размерность: <math> h'_i = M H_j (h^j_i) = [h^1_i...h^J_i] </math> | 4. Затем необходима конкатенация, чтобы вернуться в исходную размерность: <math> h'_i = M H_j (h^j_i) = [h^1_i...h^J_i] </math> | ||
| − | 5. Добавим сквозные связи (англ. ''skip connection'') - по факту просто добавление из входного вектора к выходному (<math>h'_i + h_i</math>). После делаем нормировку уровня (англ. ''layer normalization''): <math>h''_i = LN(h'_i + h_i; \mu_1, \sigma_1)</math>. У нее два обучаемых параметра, для каждой размерности вектора вычисляется среднее и дисперсия. | + | 5. Добавим сквозные связи (англ. ''skip connection'') {{---}} по факту просто добавление из входного вектора к выходному (<math>h'_i + h_i</math>). После делаем нормировку уровня (англ. ''layer normalization''): <math>h''_i = \mathrm{LN}(h'_i + h_i; \mu_1, \sigma_1)</math>. У нее два обучаемых параметра, для каждой размерности вектора вычисляется среднее и дисперсия. |
| − | 6. Теперь добавим преобразование, которое будет обучаемым - полносвязную | + | 6. Теперь добавим преобразование, которое будет обучаемым {{---}} полносвязную двухслойную нейронную сеть: |
| − | <math> h'''_i = W_2 ReLU (W_1 h''_i + b_1) + b_2 </math> | + | <math> h'''_i = W_2 \mathrm{ReLU} (W_1 h''_i + b_1) + b_2 </math> |
| − | 7. Повторим пункт 5 еще раз: добавим сквозную связь и нормировку уровня: <math>z_i = LN(h'''_i + h''_i; \mu_2, \sigma_2)</math> | + | 7. Повторим пункт 5 еще раз: добавим сквозную связь и нормировку уровня: <math>z_i = \mathrm{LN}(h'''_i + h''_i; \mu_2, \sigma_2)</math> |
После, в кодирующем компоненте пункты кодировщика 3-7 повторяются еще несколько раз, преобразовывая друг за другом из контекста контекст. Тем самым мы обогащаем модель и увеличиваем в ней количество параметров. | После, в кодирующем компоненте пункты кодировщика 3-7 повторяются еще несколько раз, преобразовывая друг за другом из контекста контекст. Тем самым мы обогащаем модель и увеличиваем в ней количество параметров. | ||
| Строка 36: | Строка 36: | ||
===Позиционное кодирование=== | ===Позиционное кодирование=== | ||
| − | [[Файл:PositionalEncoding.png| | + | [[Файл:PositionalEncoding.png|400px|thumb|right|Визуализация работы позиционного кодирования<ref>http://www.machinelearning.ru/wiki/index.php</ref>]] |
| − | Позиционное кодирование (англ. ''positional encoding'') - позволяет модели получить информацию о порядке элементов в последовательности путем прибавления специальных меток к вектору входных элементов. Позиции элементов <math>i</math> кодируются векторами <math>p_i</math>, <math>i = 1, 2, ..., n</math>, так, что чем больше <math>|i - j|</math>, тем больше <math>||p_i - p_j||</math>, и <math>n</math> не ограничено: | + | Позиционное кодирование (англ. ''positional encoding'') {{---}} позволяет модели получить информацию о порядке элементов в последовательности путем прибавления специальных меток к вектору входных элементов. Позиции элементов <math>i</math> кодируются векторами <math>p_i</math>, <math>i = 1, 2, ..., n</math>, так, что чем больше <math>|i - j|</math>, тем больше <math>||p_i - p_j||</math>, и <math>n</math> не ограничено: |
| − | <math>p_{(i, s)} = \sin(i \cdot 10000^{\frac{-2s}{d_{model}}})</math>, | + | <math>p_{(i, s)} = \sin \left(i \cdot 10000^{\frac{-2s}{d_{model}}}\right)</math>, |
| − | <math>p_{(i, s + \frac{d}{2})} = \cos(i \cdot 10000^{\frac{-2s}{d_{model}}})</math> | + | <math>p_{(i, s + \frac{d}{2})} = \cos \left(i \cdot 10000^{\frac{-2s}{d_{model}}}\right)</math> |
===Self-attention=== | ===Self-attention=== | ||
| Строка 54: | Строка 54: | ||
Далее считаем важность влияния элемента <math>x_j</math> для кодирования элемента <math>x_i</math>: | Далее считаем важность влияния элемента <math>x_j</math> для кодирования элемента <math>x_i</math>: | ||
<math>w_{ji}=\frac{ | <math>w_{ji}=\frac{ | ||
| − | \exp(\frac{\langle q_i, k_j \rangle}{\sqrt{d}}) | + | \exp \left(\frac{\langle q_i, k_j \rangle}{\sqrt{d}} \right) |
}{ | }{ | ||
| − | \sum_{p=1}^n \exp(\frac{\langle q_i, k_p \rangle}{\sqrt{d}}) | + | \sum_{p=1}^n \exp \left(\frac{\langle q_i, k_p \rangle}{\sqrt{d}} \right) |
}</math>, | }</math>, | ||
| − | где <math>d</math> - размерность векторов <math>q_i</math> и <math>k_j</math>, а <math>n</math> - число элементов во входной последовательности. | + | где <math>d</math> {{---}} размерность векторов <math>q_i</math> и <math>k_j</math>, а <math>n</math> {{---}} число элементов во входной последовательности. |
| − | Таким образом, новое представление элемента <math>x_i</math> считаем как взвешенную сумму векторов значения: <math>z_i = Attn(W_q x_i, W_k X, W_v X) = \sum_{p=1}^n w_{p i} v_p</math>, где <math>X = (x_1, x_2, ..., x_n)</math> - входные векторы. По итогу мы перемешиваем все входные векторы, чтобы получить новые векторы всех элементов, где каждый элемент зависит от всех входных элементов. | + | Таким образом, новое представление элемента <math>x_i</math> считаем как взвешенную сумму векторов значения: <math>z_i = \mathrm{Attn}(W_q x_i, W_k X, W_v X) = \sum_{p=1}^n w_{p i} v_p</math>, где <math>X = (x_1, x_2, ..., x_n)</math> {{---}} входные векторы. По итогу мы перемешиваем все входные векторы, чтобы получить новые векторы всех элементов, где каждый элемент зависит от всех входных элементов. |
===Multi-headed self-attention=== | ===Multi-headed self-attention=== | ||
| Строка 69: | Строка 69: | ||
То есть параллельно независимо несколько раз делаем attention. Потом результат каждого attention по элементам конкатенируем, затем сжимаем получившуюся матрицу и получаем для каждого элемента свой вектор той же размерности. | То есть параллельно независимо несколько раз делаем attention. Потом результат каждого attention по элементам конкатенируем, затем сжимаем получившуюся матрицу и получаем для каждого элемента свой вектор той же размерности. | ||
| − | <math>с^j = Attn(W^j_q q, W^j_k X, W^j_v X)</math>, где <math>j = 1...J</math>, <math>J</math> - | + | <math>с^j = \mathrm{Attn}(W^j_q q, W^j_k X, W^j_v X)</math>, где <math>j = 1...J</math>, <math>J</math> {{---}} число разных моделей внимания, <math>X = (x_1, x_2, ..., x_n)</math> {{---}} входные векторы, а <math>W</math> {{---}} обучаемые матрицы. |
==Архитектура трансформера-декодировщика== | ==Архитектура трансформера-декодировщика== | ||
| − | [[Файл:TransformerDecoderArchitecture.png|150px|thumb|left|Архитектура трансформера-декодировщика]] | + | [[Файл:TransformerDecoderArchitecture.png|150px|thumb|left|Архитектура трансформера-декодировщика<ref>https://arxiv.org/abs/1706.03762</ref>]] |
На вход декодировщику подается выход кодировщика. Главное отличие архитектуры декодировщика заключается в том, что дополнительно имеется attention к вектору, который получен из последнего блока кодирующего компонента. Компонент декодировщика тоже многослойный и каждому блоку компонента на вход подается вектор именно с последнего блока кодирующего компонента. Разберем по порядку этапы работы декодировщика: | На вход декодировщику подается выход кодировщика. Главное отличие архитектуры декодировщика заключается в том, что дополнительно имеется attention к вектору, который получен из последнего блока кодирующего компонента. Компонент декодировщика тоже многослойный и каждому блоку компонента на вход подается вектор именно с последнего блока кодирующего компонента. Разберем по порядку этапы работы декодировщика: | ||
| Строка 80: | Строка 80: | ||
2. Далее идет этап многомерного самовнимания: линейная нормализация и multi-headed self-attention. Особенность в том, что в attention ключи и значения применяются не ко всем векторам, а только к тем, значения которых уже синтезировали (<math>H_t</math>): | 2. Далее идет этап многомерного самовнимания: линейная нормализация и multi-headed self-attention. Особенность в том, что в attention ключи и значения применяются не ко всем векторам, а только к тем, значения которых уже синтезировали (<math>H_t</math>): | ||
| − | <math> h'_t = LN \circ M H_j \circ Attn(W^j_q h_t, W^j_k H_t, W^j_v H_t) </math> | + | <math> h'_t = \mathrm{LN} \circ M H_j \circ \mathrm{Attn}(W^j_q h_t, W^j_k H_t, W^j_v H_t) </math> |
3. На следующем этапе мы делаем многомерное внимание на кодировку <math>Z</math>, результат работы компонента кодировщика: | 3. На следующем этапе мы делаем многомерное внимание на кодировку <math>Z</math>, результат работы компонента кодировщика: | ||
| − | <math> h''_t = LN \circ M H_j \circ Attn(W^j_q h_t, W^j_k Z, W^j_v Z) </math> | + | <math> h''_t = \mathrm{LN} \circ M H_j \circ \mathrm{Attn}(W^j_q h_t, W^j_k Z, W^j_v Z) </math> |
4. Линейная полносвязная сеть (по аналогии, как и в кодировщике): | 4. Линейная полносвязная сеть (по аналогии, как и в кодировщике): | ||
| − | <math> y_t = LN \circ FNN(h''_t) </math> | + | <math> y_t = \mathrm{LN} \circ FNN(h''_t) </math> |
5. Линейный предсказывающий слой: | 5. Линейный предсказывающий слой: | ||
| − | <math> p(\tilde w|t) = | + | <math> p(\tilde w|t) = \mathrm{SoftMax}_{\tilde w}(W_y y_t + b_y) </math>, <math> W_y </math> {{---}} обучаемая матрица весовых коэффицентов, <math> b_y </math> {{---}} обучаемый вектор смещения |
| − | Последний этап выполняется только после того, когда повторились пункты 1-4 для всех декодировщиков. На выходе получаем вероятности классов, по факту решаем для каждого класса задачу многоклассовой классификации, для того, чтобы понять какие элементы лучше поставить на каждые позиции. В самом конце происходит генерация самих элементов: <math> {\tilde w}_t = arg | + | Последний этап выполняется только после того, когда повторились пункты 1-4 для всех декодировщиков. На выходе получаем вероятности классов, по факту решаем для каждого класса задачу многоклассовой классификации, для того, чтобы понять какие элементы лучше поставить на каждые позиции. В самом конце происходит генерация самих элементов: <math> {\tilde w}_t = \mathrm{arg max}_{\tilde w} p(\tilde w|t) </math>, пока не сгенерируется слово обозначающее конец последовательности. |
==Источники информации== | ==Источники информации== | ||
Версия 00:17, 11 июня 2022
Трансформер (англ. transformer) — архитектура глубоких нейронных сетей, основанная на механизме внимания без использования рекуррентных нейронных сетей (сокр. RNN). Самое большое преимущество трансформеров по сравнению с RNN заключается в их высокой эффективности в условиях параллелизации. Впервые модель трансформера была предложена в статье Attention is All You Need[1] от разработчиков Google в 2017 году.
Содержание
Архитектура трансформера
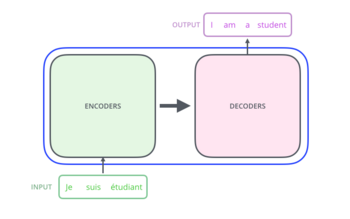
Устройство трансформера состоит из кодирующего и декодирующего компонентов. На вход принимается некая последовательность, создается ее векторное представление (англ. embedding), векторизованная последовательность поступает в кодирующий компонент, а затем декодирующий компонент получает на вход часть этой последовательности и выход кодирующего. В результате получается новая выходная последовательность.
Кодирующий компонент – это стек кодировщиков (англ. encoders), а декодирующий компонент – это стек декодировщиков (англ. decoders). Каждый кодировщики последовательно передает результат своей работы следующему кодировщику на вход. Декодировщики последовательно передают друг другу на вход результат работы вместе с результатом кодирующего компонента.
Ниже рассмотрим архитектуру кодировщика и декодировщика подробнее.
Архитектура трансформера-кодировщика
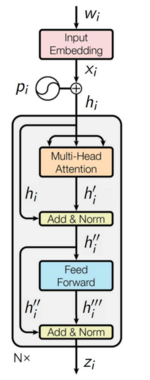
Рассмотрим последовательно шаг за шагом этапы кодировщика:
1. На вход поступает последовательность элементов , по ней создается последовательность эмбедингов, где каждый это векторное представление элемента .
2. Добавляются позиционные векторы : , . Это необходимо для того, чтобы отобразить информацию о позиции элемента в исходной последовательности. Основное свойство позиционного кодирования — чем дальше два вектора будут стоять друг от друга в последовательности, тем больше между ними будет расстояние. Более подробное устройство позиционного кодирования будет рассмотрено ниже.
3. Полученный вектор подается на вход в блок многомерного самовнимания (англ. multi-headed self-attention). , где — обучаемые матрицы, для запроса, для ключа, для значения. Подробное объяснения работы механизма self-attention будет разобрано ниже.
4. Затем необходима конкатенация, чтобы вернуться в исходную размерность:
5. Добавим сквозные связи (англ. skip connection) — по факту просто добавление из входного вектора к выходному (). После делаем нормировку уровня (англ. layer normalization): . У нее два обучаемых параметра, для каждой размерности вектора вычисляется среднее и дисперсия.
6. Теперь добавим преобразование, которое будет обучаемым — полносвязную двухслойную нейронную сеть:
7. Повторим пункт 5 еще раз: добавим сквозную связь и нормировку уровня:
После, в кодирующем компоненте пункты кодировщика 3-7 повторяются еще несколько раз, преобразовывая друг за другом из контекста контекст. Тем самым мы обогащаем модель и увеличиваем в ней количество параметров.
Позиционное кодирование
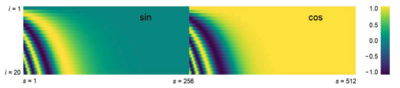
Позиционное кодирование (англ. positional encoding) — позволяет модели получить информацию о порядке элементов в последовательности путем прибавления специальных меток к вектору входных элементов. Позиции элементов кодируются векторами , , так, что чем больше , тем больше , и не ограничено: ,
Self-attention
Self-Attention — разновидность механизма внимания, задачей которой является выявление закономерности между входными данными.
Будем для каждого элемента обучать три вектора:
- Запрос (query)
- Ключ (key)
- Значение (value)
Векторы и будем использовать, что посчитать важность элемента для элемента . Чтобы понять, насколько для пересчета вектора элемента важен элемент мы берем (вектор ключа элемента ) и умножаем на (вектор запроса элемента ). Так мы скалярно перемножаем вектор запроса на все векторы ключей, тем самым понимаем, насколько каждый входной элемент нам нужен, чтобы пересчитать вектор элемента .
Далее считаем важность влияния элемента для кодирования элемента : , где — размерность векторов и , а — число элементов во входной последовательности.
Таким образом, новое представление элемента считаем как взвешенную сумму векторов значения: , где — входные векторы. По итогу мы перемешиваем все входные векторы, чтобы получить новые векторы всех элементов, где каждый элемент зависит от всех входных элементов.
Multi-headed self-attention
Multi-headed self-attention — улучшенная модификация self-attention.
Слой внимания снабжается множеством «подпространств представлений» (англ. representation subspaces). Теперь у нас есть не один, а множество наборов матриц запроса/ключа/значения. Каждый из этих наборов создается случайным образом. Далее после обучения каждый набор используется для отображения входящих векторов в разных подпространствах представлений. Также появляется способность модели фокусироваться на разных аспектах входной информации.
То есть параллельно независимо несколько раз делаем attention. Потом результат каждого attention по элементам конкатенируем, затем сжимаем получившуюся матрицу и получаем для каждого элемента свой вектор той же размерности.
, где , — число разных моделей внимания, — входные векторы, а — обучаемые матрицы.
Архитектура трансформера-декодировщика
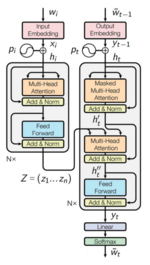
На вход декодировщику подается выход кодировщика. Главное отличие архитектуры декодировщика заключается в том, что дополнительно имеется attention к вектору, который получен из последнего блока кодирующего компонента. Компонент декодировщика тоже многослойный и каждому блоку компонента на вход подается вектор именно с последнего блока кодирующего компонента. Разберем по порядку этапы работы декодировщика:
1. Для того, чтобы распараллелить декодировщик и уйти от рекуррентности, но тем не менее генерировать элементы друг за другом, используется прием маскирования данных из будущего. Идея в том, что мы запрещаем себе подглядывать в те элементы, которые еще не сгенерированы с учетом порядка. Когда генерируем элемент под номером , имеем право смотреть только первые элементов: ;
2. Далее идет этап многомерного самовнимания: линейная нормализация и multi-headed self-attention. Особенность в том, что в attention ключи и значения применяются не ко всем векторам, а только к тем, значения которых уже синтезировали ():
3. На следующем этапе мы делаем многомерное внимание на кодировку , результат работы компонента кодировщика:
4. Линейная полносвязная сеть (по аналогии, как и в кодировщике):
5. Линейный предсказывающий слой: , — обучаемая матрица весовых коэффицентов, — обучаемый вектор смещения
Последний этап выполняется только после того, когда повторились пункты 1-4 для всех декодировщиков. На выходе получаем вероятности классов, по факту решаем для каждого класса задачу многоклассовой классификации, для того, чтобы понять какие элементы лучше поставить на каждые позиции. В самом конце происходит генерация самих элементов: , пока не сгенерируется слово обозначающее конец последовательности.