Обсуждение участника:Gen05

Выбор признаков (Feature selection)

Уменьшение размерности

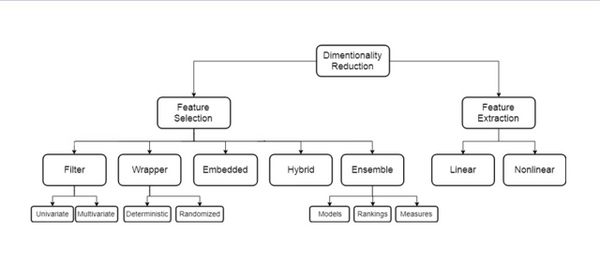
Под уменьшением размерности (англ. dimensionality reduction) в машинном обучении подразумевается уменьшение числа признаков набора данных. Наличие в нем признаков избыточных, неинформативных или слабо информативных может понизить эффективность модели, а после такого преобразования она упрощается, и соответственно уменьшается размер набора данных в памяти и ускоряется работа алгоритмов ML на нем. Уменьшение размерности может быть осуществлено методами выбора признаков (англ. feature selection) или выделения признаков (англ. feature extraction).

Определение:

Объекты описаны признаками $F = (f_1, . . . , f_n)$. Задачей является построить множество признаков $G = (g_1, ... , g_k) : k < n$ (часто $k << n$), переход к которым сопровождается наименьшей потерей информации.

Зачем нужно

• Ускорение обучения и обработки
• Борьба с шумом и мультиколлинеарностью
• Интерпретация и визуализация данных

Определение:

Проклятие размерности (curse of dimensionality) — это набор проблем, возникающих с ростом размерности Увеличиваются требования к памяти и вычислительной мощности Данные становятся более разреженными Проще найти гипотезы, не имеющие отношения к реальности

Когда применяется

Замечание:
Уменьшение размерности — шаг в предобработке данных

• Нужно использовать меньше памяти для хранения данных
• Нужно уменьшить время обработки
• Нужно увеличить качество обработки
• Нужно понять природу признаков

Методы уменьшения размерности

Два основных подхода уменьшения размерности

Выбор признаков (feature selection) включает методы, для которых $G ⊂ F$. Они:

• быстро работают;
• не могут «выдумывать» сложных признаков.

Извлечение признаков (feature extraction) включает все другие методы (в том числе даже те, у которых $k > n$).

• в целом, дольше работают;
• могут извлекать сложные признаки.

Цели извлечения и выбора признаков

• Уменьшение числа ресурсов, требуемых для обработки больших наборов данных
• Поиск новых признаков
• Эти признаки могут быть линейными и нелинейными относительно исходных

Цели выбора признаков:

• Уменьшение переобучения и улучшение качества предсказания
• Улучшение понимания моделей

Типы ненужных признаков

Существуют также два типа признаков, которые не являются необходимыми:

• Избыточные (redundant) признаки не привносят дополнительной информации относительно существующих
• Нерелевантные (irrelevant) признаки просто неинформативны

Встроенные методы

Схема встроенного метода

Классификация методов выбора признаков

• Встроенные методы (embedded)
• Фильтрующие методы (filter)
  • Одномерные (univariate)
  • Многомерные (multivariate)
• Методы-обертки (wrapper)
  • Детерминированные (deterministic)
  • Стохастические (stochastic)
• Гибридные и ансамблирующие методы

Встроенные методы

Процесс работы встроенных методов

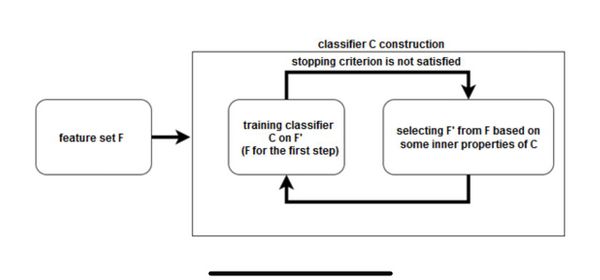
Группа встроенных методов (англ. embedded methods) очень похожа на оберточные методы, но для выбора признаков используется непосредственно структуру некоторого классификатора. В оберточных методах классификатор служит только для оценки работы на данном множестве признаков, тогда как встроенные методы используют какую-то информацию о признаках, которую классификаторы присваивают во время обучения.

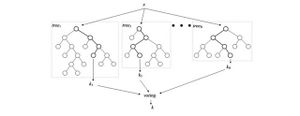
Одним из примеров встроенного метода является реализация на случайном лесе: каждому дереву на вход подаются случайное подмножество данных из датасета с каким-то случайным набор признаков, в процессе обучения каждое из деревьев решений производит "голосование" за релевантность его признаков, эти данные агрегируются, и на выходе получаются значения важности каждого признака набора данных. Дальнейший выбор нужных нам признаков уже зависит от выбранного критерия отбора.

Встроенные методы используют преимущества оберточных методов и являются более эффективными, при этом на отбор тратится меньше времени, уменьшается риск переобучения, но т.к. полученный набор признаков был отобран на основе знаний о классификаторе, то есть вероятность, что для другого классификатора это множество признаков уже не будет настолько же релевантным.

Пример: случайный лес

Случайный лес

• Учитывать число вхождений признака в дерево.
• Учитывать глубину вершины вхождения признака в дерево.

Пример: SVM-RFE

1. Обучить SVM на обучающем подмножестве
2. Установить веса признаков, равными модулям соответствующих коэффициентов
3. Отранжировать признаки согласно их весам
4. Выбросить некоторое число признаков с наименьшими весами
5. Повторять, пока не останется нужное число признаков

Методы-обертки

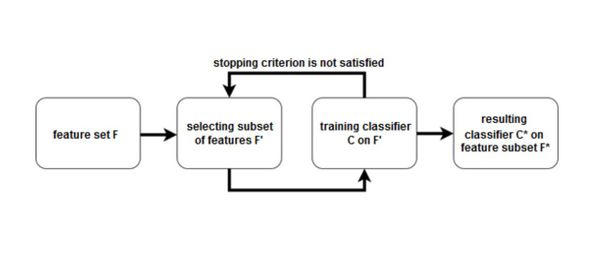
Схема метода-обертки

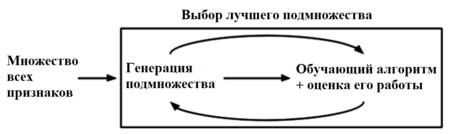
Метод-обертка (wrapper method) использует алгоритм (классификатор или регрессор) для оценки качества получаемого подмножества признаков и использует алгоритмы дискретной оптимизации для поиска оптимального подмножества признаков.

Классификация методов-оберток

• Детерминированные:
  • SFS (sequential forward selection)
  • SBE (sequential backward elimination)
  • SVM-RFE
  • Перестановочная полезность (Permutation importance)
• Стохастические — сводят задачу выбора признаков к задаче оптимизации в пространстве бинарных векторов:
• Поиск восхождением на холм
  • Генетические алгоритмы
  • ...

Анализ методов-оберток

Достоинства:

• Более высокая точность, чем у фильтров
• Используют отношения между признаками
• Оптимизируют качество предсказательной модели в явном виде

Недостатки:

• Очень долго работают
• Могут переобучиться при неправильной работе с разбиением набора данных

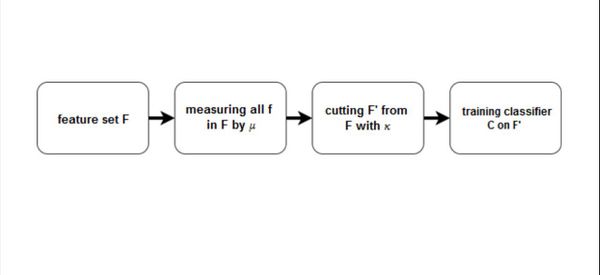
Фильтры

Фильтры (filter methods) оценивают качество отдельных признаков или подмножеств признаков и удаляют худшие

Две компоненты:

• мера значимости признаков μ
• правило обрезки κ определяет, какие признаки удалить на основе μ

Схема фильтрующих методов

Классификация фильтрующих методов

• Одномерные (univariate):
  • Евклидово расстояние
  • Коэффициент корреляции (Пирсона или Спирмена)
  • Попарные расстояния (внутренние или внешние)
  • Условная дисперсия
  • Прирост информации (IG)
  • Индекс Джини
  • χ2
• Многомерные (multivariate):
  • Выбор признаков на основе корреляций (CFS)
  • Фильтр марковского одеяла (MBF)

Корреляция

Коэффициент корреляции Пирсона

Файл:Таблица 6.jpg

600px

Коэффициент корреляции Спирмана

1. Отсортировать объекты двумя способами (по каждому из признаков).
2. Найти ранги объектов для каждой сортировки.
3. Вычислить корреляцию Пирсона между векторами рангов.

Правило обрезки κ

• Число признаков
• Порог значимости признаков
• Интегральный порог значимости признаков
• Метод сломанной трости
• Метод локтя

Анализ одномерных фильтров

Преимущества:

• Исключительно быстро работают
• Позволяют оценивать значимость каждого признака

Недостатки:

• Порог значимости признаков
• Игнорируют отношения между признаками и то, что реально использует предсказательная модель

Анализ многомерных фильтров

Преимущества:

• Работают достаточно быстро
• Учитывают отношения между признаками

Недостатки:

• Работают существенно дольше фильтров
• Не учитывают то, что реально использует предсказательная модель

Гибриды и ансамбли

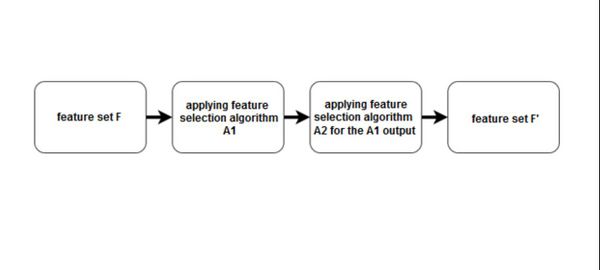
Гибридный подход

Будем комбинировать подходы, чтобы использовать их сильные стороны Самый частый вариант:

• сначала применим фильтр (или набор фильтров), отсеяв лишние признаки
• затем применим метод-обертку или встроенный метод

Схема гибридного подхода

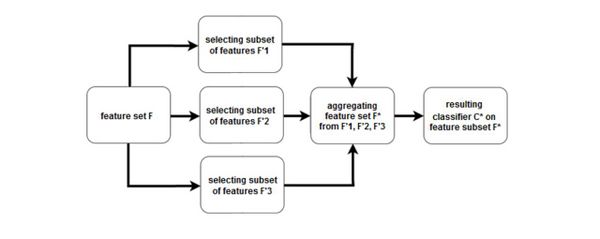
Ансамблирование в выборе признаков

Подход к ансамблированию состоит в построении ансамбля алгоритмов выбора признаков

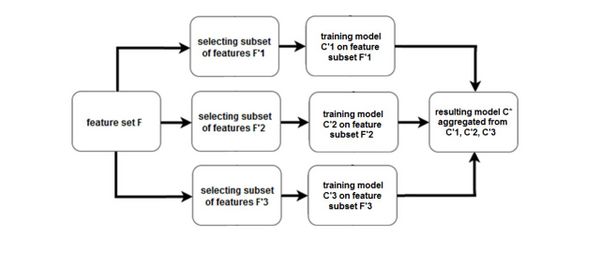
Ансамбль на уровне моделей

Строим ансамбль предсказательных моделей

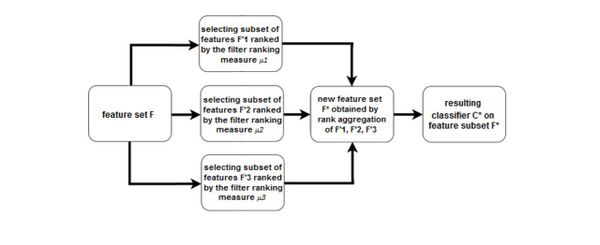
Ансамбль на уровне ранжирований

Объединяем ранжирования

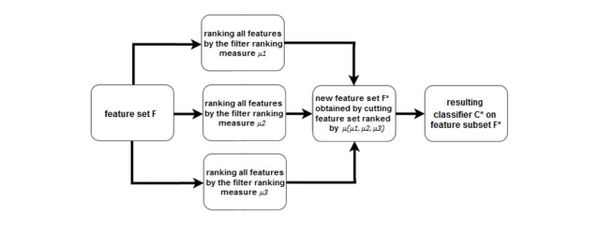
Ансамбль на уровне мер значимости

Объединяем меры значимости

Анализ гибридных и ансамблирующих методов

Преимущества:

• Чаще всего лучше по времени и по качеству

Недостатки:

• Иногда теряется интерпретируемость
• Иногда требуется заботиться о проблеме переобучения