|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | {{Задача | | {{Задача |
| | |definition = Дано две квадратных матрицы <tex>A_{[n \times n]}</tex> и <tex>B_{[n \times n]}</tex>, | | |definition = Дано две квадратных матрицы <tex>A_{[n \times n]}</tex> и <tex>B_{[n \times n]}</tex>, |
Текущая версия на 19:14, 4 сентября 2022
| Задача: |
| Дано две квадратных матрицы [math]A_{[n \times n]}[/math] и [math]B_{[n \times n]}[/math],
состоящие из нулей и единиц. Нужно найти их произведение. При этом, все операции выполняются по модулю [math]2[/math]. |
Простое решение
Если мы будем считать произведение матриц [math]C = A \cdot B[/math] по определению [math]\left(c_{i, j} = \sum\limits_{k = 1}^n a_{i,k}b_{k,j}\right)[/math], то сложность работы алгоритма составит [math]O(n^3)[/math] — каждый из [math]n^2[/math] элементов результирующей матрицы [math]C[/math] вычисляется за время, пропорциональное [math]n[/math].
Сейчас будет показано, как немного уменьшить это время.
Сжатие матриц
Для выполнения сжатия матриц выполним следующий предподсчёт : для всех возможных пар двоичных векторов длины [math]k[/math] подсчитаем и запомним их скалярное произведение по модулю [math]2[/math].
Возьмём первую матрицу. разделим каждую её строку на куски размера [math]k[/math]. Для каждого куска определим номер двоичного вектора, который соответствует числам, находящимся на этом куске. Если кусок получился неравным по длине [math]k[/math](последний кусок строки), то будем считать, что в конце в нём идут не влияющие на умножение нули. Получим матрицу [math]A'_{n \times \lceil\frac{n}{k} \rceil}[/math].
Аналогично поступим с матрицей [math]B[/math], вместо строк деля столбцы. Получим матрицу [math]B'_{\lceil\frac nk\rceil\times n}[/math].
Теперь, если вместо произведения матриц [math]A[/math] и [math]B[/math] считать произведение новых матриц [math]A'[/math] и [math]B'[/math], воспользовавшись посчитанными скалярными произведениями, то каждый элемент матрицы [math]C[/math] будет получаться уже за время, пропорциональное [math]\lceil \dfrac{n}{k} \rceil[/math] вместо [math]n[/math], и время произведения матриц сократится с [math]O(n^3)[/math] до [math]O(n^2 \cdot\dfrac nk) = O(\dfrac{n^3}{k}) [/math].
Оценка сложности алгоритма и выбор k
Оценим асимптотику данного алгоритма.
- Предподсчёт скалярных произведений работает за [math]O(2^{2k}k)[/math].
- Создание матриц [math]A'[/math] и [math]B'[/math] — [math]O(n^2)[/math].
- Перемножение полученных матриц — [math]O(\dfrac{n^3}{k})[/math].
Итого: [math]O(2^{2k}k) + O(\dfrac{n^3}{k})[/math].
Выбрав [math]k = \log n [/math], получаем требуемую асимптотику [math]O(n^2 \log n) + O(\dfrac{n^3}{\log n}) = O(\dfrac{n^3}{\log n})[/math]
Пример работы алгоритма
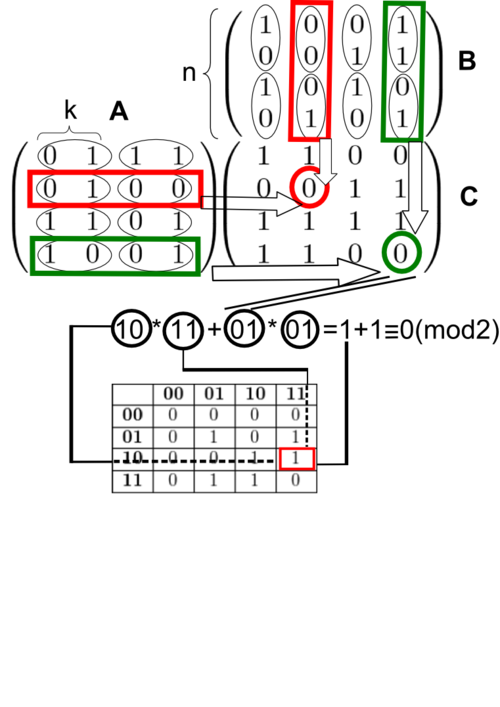
Рассмотрим работу алгоритма на примере перемножения двух матриц [math] A [/math] и [math] B [/math], где
[math] A = [/math]
[math]
\left(\begin{array}{cccc}
0 & 1 & 1 & 1 \\
0 & 1 & 0 & 0 \\
1 & 1 & 0 & 1 \\
1 & 0 & 0 & 1
\end{array}\right)
[/math]
, [math] B = [/math]
[math]
\left(\begin{array}{cccc}
1 & 0 & 0 & 1 \\
0 & 0 & 1 & 1 \\
1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1
\end{array}\right)
[/math]
[math] k = \log_2 n = \log_2 4 = 2[/math], то предподсчитаем все скалярные произведения:
Для удобства каждому битовому вектору будет соответствовать двоичное число с ведущими нулями, т.е. в данном случае имеем числа [math] 00 [/math], [math] 01 [/math], [math] 10 [/math], [math] 11 [/math]. Ниже приведена таблица, в которой записаны все искомые произведения:
[math]
\begin{array}{|c|c|c|c|c|}
\hline
& \textbf{00} & \textbf{01} & \textbf{10} & \textbf{11} \\
\hline
\textbf{00} & 0 & 0 & 0 & 0 \\
\hline
\textbf{01} & 0 & 1 & 0 & 1 \\
\hline
\textbf{10} & 0 & 0 & 1 & 1 \\
\hline
\textbf{11} & 0 & 1 & 1 & 0\\
\hline
\end{array}
[/math]
Согласно соглашению относительно битовых векторов и двоичных чисел получим новые матрицы [math] A' [/math] и [math] B' [/math]:
[math] A' = [/math]
[math]
\left(\begin{array}{cccc}
01 & 11 \\
01 & 00 \\
11 & 01 \\
10 & 01
\end{array}\right)
[/math]
,
[math] B' = [/math]
[math]
\left(\begin{array}{cccc}
10 & 00 & 01 & 11 \\
10 & 01 & 10 & 01
\end{array}\right)
[/math]
Перемножим эти матрицы по модулю два с использованием нашего предпосчета:
[math] C = A' \times B' = [/math]
[math]
\left(\begin{array}{cccc}
1 & 1 & 0 & 0 \\
0 & 0 & 1 & 1 \\
1 & 1 & 1 & 1 \\
1 & 1 & 0 & 0
\end{array}\right)
[/math]
Матрица [math] C [/math] — искомая.
Источники информации
- Gregory V. Bard — Accelerating Cryptanalysis with the Method of Four Russians. July 22, 2006. Страница 5