|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | <tex dpi = "200">P \mid pmtn, r_i \mid L_{max}</tex> | | <tex dpi = "200">P \mid pmtn, r_i \mid L_{max}</tex> |
| | | | |
Текущая версия на 19:27, 4 сентября 2022
[math]P \mid pmtn, r_i \mid L_{max}[/math]
| Задача: |
- Имеется [math]M[/math] однородных машин, работающих параллельно.
- Есть [math]n[/math] работ, каждое имеет своё время появления [math]r_i[/math] и время окончания [math]d_i[/math].
- Работа может быть прервана и продолжена позже.
Необходимо составить такое расписание, чтобы значение [math]L_{max} = \max\limits_{i=1\ldots n} (C_i - d_i)[/math] было минимальным. |
Решение
Сведем эту задачу к поиску максимального потока в сети, построенной указанным ниже образом.
Пусть [math]t_1 \lt t_2 \lt \ldots \lt t_r[/math] - упорядоченная последовательность [math]r_i[/math] и [math]d_i[/math]. Определим интервалы [math]I_K = [t_K; t_{K+1}][/math] с длиной [math]T_K = t_{K+1} - t_K[/math] для всех [math]K = 1 \ldots r-1[/math].
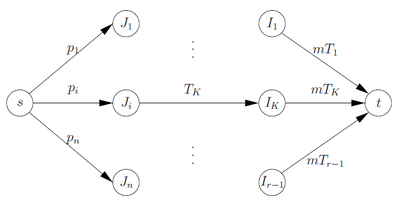
Работам [math]J_i[/math] сопоставим свой тип вершин, а интервалам [math]I_K[/math] свой. Добавим две фиктивные вершины [math]s[/math] и [math]t[/math]. Вершина [math]s[/math] соединена с вершинами [math]J_i[/math] ребрами с пропускной способностью [math]p_i[/math], вершина [math]t[/math] соединена с вершинами [math]I_K[/math] ребрами с пропускной способностью [math]mT_K[/math]. Ребро между вершиной [math]J_i[/math] и вершиной [math]I_K[/math] существует, если [math]r_i \leqslant t_K, t_{K+1} \leqslant d_i[/math]. Пропускная способность этого ребра - [math]T_K[/math].
Нетрудно понять, что расписание существует, если максимальный поток через эту сеть равен [math]\sum\limits_{i=1}^n p_i[/math].
Если это так, то поток [math]x_{iK}[/math] на дуге [math](J_i, I_K)[/math] соответствует тому, что работа [math]J_i[/math] будет выполняться во временном интервале [math]I_K[/math], и будет справедливо следующее:
- [math]\sum\limits_{K=1}^{r-1} x_{iK} = p_i, i = 1 \ldots n[/math]
- [math]\sum\limits_{i=1}^n x_{iK} \leqslant mT_K, K = 1 \ldots r - 1[/math]
- [math]x_{iK} \leqslant T_K[/math] для всех ребер [math](J_i, I_K)[/math]
Исходя из этого, расписание строится выполнением работы [math]J_{iK}[/math] с временем выполнения [math]x_{iK} \gt 0[/math] в интервале [math]I_K[/math].
Т.к. сеть содержит [math]O(n)[/math] элементов, значит максимальный поток в ней можно найти за [math]O(n^3)[/math]. Кроме того, построение "окон" выполнения работ займет [math]O(n^2)[/math]. Т.о. указанный выше алгоритм потребует [math]O(n^3)[/math] операций.
Для решения данной задачи мы используем бинпоиск по [math]L[/math] значениям, а значит, получаем алгоритм с [math]\varepsilon[/math]-приближенной сложностью [math]O (n^3(\log(n) + \log(\cfrac{1}{\varepsilon}) + \log(\max\limits_{j=1 \ldots n} (p_j))) [/math], потому как [math]L_{max}[/math], ограничен [math]n\max\limits_{j=1 \ldots n} (p_j)[/math]