Реляционная алгебра: операции над множествами — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
В этом разделе будут описаны операции над множествами в рамках [[Реляционная_алгебра|реляционной алгебры]]. В соответствии с определением, для каждой операции необходимо указать способ построения заголовка, тела отношения, а также условия применимости, если такие есть. | В этом разделе будут описаны операции над множествами в рамках [[Реляционная_алгебра|реляционной алгебры]]. В соответствии с определением, для каждой операции необходимо указать способ построения заголовка, тела отношения, а также условия применимости, если такие есть. | ||
Текущая версия на 19:44, 4 сентября 2022
В этом разделе будут описаны операции над множествами в рамках реляционной алгебры. В соответствии с определением, для каждой операции необходимо указать способ построения заголовка, тела отношения, а также условия применимости, если такие есть.
Простые операции
Из теории множеств в реляционную алгебру естественным образом переходят операции:
- — объединение;
- — пересечение;
- — разность.
Эти операции по определению применимы только к отношениям с одинаковыми заголовками. В результате получается отношение с таким же заголовком и телом, полученным в соответствии с множественной операцией. Иначе говоря, заголовок остается тем же, а над телами отношений производится соответствущая множественная операция (объединение, пересечение, вычитание и прочие).
Примеры
- Объединение отношений:
Как и в случае множественных операций, дубликаты учитываются ровно по одному разу.
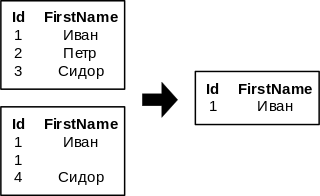
- Пересечение отношений:
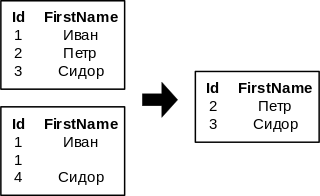
- Разность отношений:
Стоит отметить, что для объединения отношений с различающимися именами атрибутов, но при равном их количестве, можно воспользоваться переименованием для того, чтобы привести заголовки к одному виду.