Реализация вычитания сумматором
Содержание
Преобразование чисел для вычитания сумматором
Что бы реализовать вычитание каскадным или двоичным каскадным сумматором, нужно сложить на нём уменьшаемое с противоположным по знаку вычитаемым, так же как и при вычитании обычных чисел. Тогда полученная сумма будет разностью данных чисел.
Инверсия знака записанного в двоичном виде числа происходит точно так же, как и в дополнительном коде.
Данное число нужно инвертировать и прибавить к нему единицу.
Например число будет записано как , так как , а
Оптимизация
Очевидно, что такой подход к вычитанию сумматором не оптимален.Что бы упростить вычисления нужно воспользоваться лишним битом переноса в сумматоре, в который посылают ноль, и послать в него единицу при вычитании и ноль при суммировании. Вместо того что бы инвертировать вычитаемое число, можно сделать XOR бита первого переноса с каждым битом вычитаемого числа.
Таким образом, можно посылать в полученный арифмометр для сложения и вычитания числа точно так же как и при сложении, только первый бит переноса будет отвечать за знак операции: 0-сложение 1-вычитание.
Пример реализация вычитания сумматором
| Условные обозначения | Изображение арифмометра | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
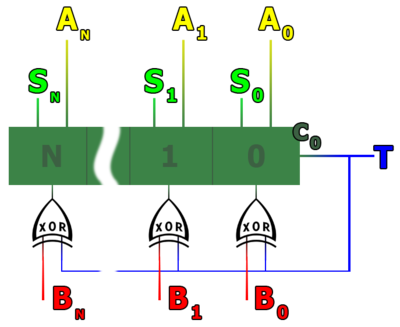
|
См. также
Сумматор
Матричный умножитель
Реализация булевой функции схемой из функциональных элементов
Ссылки
Subtractor
Negative Numbers and Binary Subtraction
Рабочий пример арифмометра