Материал из Викиконспекты
В троичной логике "лжи" и "истине" соответствует [math]-[/math] и [math]+[/math]. Третьему состоянию соответствует [math]0[/math].
Мы будем рассматривать простую троичную функциональную схему — троичный сумматор. Поэтому, вместо обозначений [math]\{-, 0, +\}[/math], мы используем [math]\{0, 1, 2\}[/math] (несимметричная троичная система счисления).
Полусумматор состоит из двух частей: сложения по модулю [math]3[/math] и переноса в следующий разряд.
Логическое сложение по модулю [math]3[/math] при одном неполном слагаемом
Для сложения одного троичного разряда с разрядом переноса.
Результат не меняется при перемене мест операндов.
| [math]\bf{x_1=x}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{s}[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
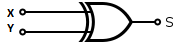
Разряд переноса при сложении с неполным слагаемым
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
| [math]\bf{x_1=x}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{c}[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
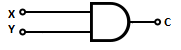
Троичный полусумматор с одним неполным слагаемым
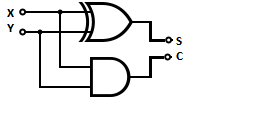
Первая ступень полного троичного сумматора.
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
| [math]\bf{x_1=x}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{z_{sum}}[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{z_{transfer}}[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
transfer содержит разряд переноса, sum содержит сумму по модулю [math]3[/math].
Троичный полусумматор в несимметричной троичной системе счисления
Троичное логическое сложение двух троичных разрядов с разрядом переноса в несимметричной троичной системе счисления.
Результат не изменяется при перемене мест операндов.
Троичный полусумматор можно рассматривать, как объединение двух бинарных троичных функций: «логического сложения по модулю [math]3[/math] в троичной несимметричной системе счисления» и «разряд переноса при сложении двух полных троичных разрядов в троичной несимметричной системе счисления».
| [math]\bf{x_1=x}[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_0=y}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{sum}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{c_{transfer}}[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
c_{transfer} — перенос в следующий разряд, несимметричный.
sum — сумма по модулю [math]3[/math], несимметричная.
Полное троичное логическое сложение с переносом в несимметричной троичной системе счисления
Полный троичный одноразрядный сумматор является неполной тернарной троичной логической функцией, так как в разряде переноса только два значения [math]0[/math] и [math]1[/math].
Результат не изменяется при перемене мест операндов.
| [math]\bf{x_0}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{x_1}[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{x_2}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
| [math]\bf{z_{sum}}[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]0[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]1[/math]
|
[math]0[/math]
|
| [math]\bf{z_{transfer}}[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]1[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]0[/math]
|
См. такжеИсточники информации


