Эта статья находится в разработке!
Недетерминированный автомат с магазинной памятью
По умолчанию будем считать автоматы с магазинной памятью недетерминированными. Если речь пойдет о детерминированном автомате, то это будет указано отдельно.
| Определение: |
Автомат с магазинной памятью --- это набор A=[math]\langle\Sigma,\Gamma,Q,s\in Q, T \subset Q, z_0 \in \Gamma, \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow \cal P[/math][math](Q \times \Gamma^*)\rangle[/math], где
- [math]\Sigma[/math] --- входной алфавит на ленте;
- [math]\Gamma[/math] --- стековый алфавит;
- [math]Q[/math] --- множество состояний автомата;
- [math]s[/math] --- стартовое состояние автомата;
- [math]T[/math] --- множество допускающих состояний автомата;
- [math]z_0[/math] --- маркер дна стека;
- [math]\delta[/math] --- функция переходов.
|
Диаграммы переходов
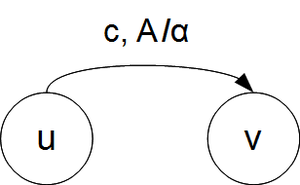
Переход: с - символ, прочитанный с ленты; A - символ, вынутый из стека;
[math]\alpha[/math] - строка, помещаемая в стек
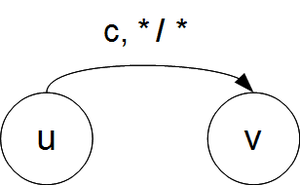
Переход по любому стековому символу, он же возвращается в стек
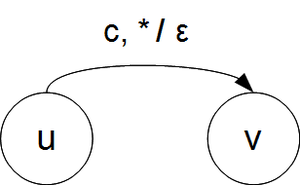
Переход по любому стековому символу, в стек кладется пустая строка
По соглашению маркер дна всегда находится на дне (за исключением случая, когда автомат является автоматом с допуском по пустому стеку). То есть, для [math]\mathcal8 q \in Q,\mathcal8 c \in \Sigma \cup \varepsilon \Rightarrow \delta(q, c, z_0) \ni \langle p, \alpha \rangle [/math], где [math]p \in Q, \alpha \in \Gamma^*, \alpha = \alpha_1z_0[/math]
Основные определения
- Мгновенное описание: [math]\langle q, \alpha, \gamma \rangle[/math], где [math]q[/math] --- текущее состояние, [math]\alpha[/math] --- остаток строки, [math]\gamma[/math] --- содержимое стека.
- Переход за один шаг обозначается как [math]\langle q, \alpha, \gamma \rangle \vdash \langle r, \beta, \xi \rangle[/math], где [math]\alpha = c\beta[/math] (возможно, [math]c=\varepsilon[/math]), [math]\gamma = \chi\gamma', \xi = \eta\gamma'[/math], [math]\langle r, \eta \rangle \in \delta(q, c, \chi)[/math]
| Определение: |
| Язык автомата с магазинной памятью [math]L(A)=\{\alpha \mid \langle s, \alpha, z_0\rangle \vdash^* \langle t, \varepsilon, \gamma \rangle, t \in T\}[/math] |
Пример
Рассмотрим недетерминированный автомат с магазинной памятью для языка [math]0^n1^n[/math].
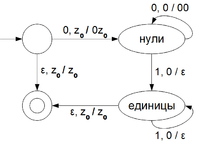
Недетерминированный МП-автомат для языка
[math]0^n1^n[/math]Детерминированный автомат с магазинной памятью
| Определение: |
Если для автомата с магазинной памятью выполняются следующие условия:
- [math]\mathcal8 q \in Q, \mathcal8 c \in \Sigma, \mathcal8 X \in \Gamma \Rightarrow \left | \delta(q, c, X)\right | \le 1[/math];
- [math]\delta(q,\varepsilon,X) \ne 0 \Rightarrow \mathcal8 c \in \Sigma : \delta(q, c, X) = \varnothing[/math],
то поведение автомата всегда определено однозначно и он называется детерминированным автоматом с магазинной памятью. |



