Алгоритм Флойда

Алгоритм Флойда (алгоритм Флойда–Уоршелла) — алгоритм нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а в случае, когда такой цикл есть, позволяет найти хотя бы один такой цикл. Алгоритм работает за $\Theta(n^3)$ времени и использует $\Theta(n^2)$ памяти. Разработан в 1962 году.

Алгоритм

Постановка задачи

Текущий (синий) путь и потенциально более короткий (красный)

Дан взвешенный ориентированный граф $G(V, E)$, в котором вершины пронумерованы от $1$ до $n$.

$\omega_{uv} = \begin{cases} \text{weight of }uv ,& \text{if } uv \in E \\ +\infty ,& \text{if } uv \notin E \end{cases}$
Требуется найти матрицу кратчайших расстояний $d$, в которой элемент $d_{ij}$ либо равен длине кратчайшего пути из $i$ в $j$, либо равен $+\infty$, если вершина $j$ не достижима из $i$.

Описание

Обозначим длину кратчайшего пути между вершинами $u$ и $v$, содержащего, помимо $u$ и $v$, только вершины из множества $\{ 1 .. i \}$ как $d_{uv}^{(i)}$, $d_{uv}^{(0)} = \omega_{uv}$.

На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер — $i$) и для всех пар вершин $u$ и $v$ вычислять $d_{uv}^{(i)} = \min(d_{uv}^{(i-1)}, d_{ui}^{(i-1)} + d_{iv}^{(i-1)})$. То есть, если кратчайший путь из $u$ в $v$, содержащий только вершины из множества $\{ 1 .. i \}$, проходит через вершину $i$, то кратчайшим путем из $u$ в $v$ является кратчайший путь из $u$ в $i$, объединенный с кратчайшим путем из $i$ в $v$. В противном случае, когда этот путь не содержит вершины $i$, кратчайший путь из $u$ в $v$, содержащий только вершины из множества $\{ 1 .. i \}$ является кратчайшим путем из $u$ в $v$, содержащим только вершины из множества $\{ 1 .. i-1 \}$.

Код (в первом приближении)

$d^{(0)}_{uv} = w$
for $i \in V$
    for $u \in V$
        for $v \in V$
            $d^{(i)}_{uv} = \min(d^{(i - 1)}_{uv}, d^{(i - 1)}_{ui} + d^{(i - 1)}_{iv})$

В итоге получаем, что матрица $d^{(n)}$ и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества $\{ 1..n \}$, что есть попросту все вершины графа. Такая реализация работает за $\Theta(n^3)$ времени и использует $\Theta(n^3)$ памяти.

Код (окончательный)

Утверждается, что можно избавиться от одной размерности в массиве $d$, т.е. использовать двумерный массив $d_{uv}$. В процессе работы алгоритма поддерживается инвариант $\rho(u, v) \leqslant d_{uv} \leqslant d_{uv}^{(i)}$, а, поскольку, после выполнения работы алгоритма $\rho(u, v) = d_{uv}^{(i)}$, то тогда будет выполняться и $\rho(u, v) = d_{uv}$.

Утверждение:

В течение работы алгоритма Флойда выполняются неравенства: $\rho(u, v) \leqslant d_{uv} \leqslant d_{uv}^{(i)}$.

$\triangleright$

После инициализации все неравенства, очевидно, выполняются. Далее, массив $d$ может измениться только в строчке 5. Докажем второе неравенство индукцией по итерациям алгоритма. Пусть также $d'_{uv}$ — значение $d_{uv}$ сразу после $i - 1$ итерации. Покажем, что $d_{uv} \leqslant d_{uv}^{(i)}$, зная, что $d'_{uv} \leqslant d_{uv}^{(i - 1)}$. Рассмотрим два случая: Значение $d_{uv}^{(i)}$ стало меньше, чем $d_{uv}^{(i - 1)}$. Тогда $d_{uv}^{(i)} = d_{ui}^{(i-1)} + d_{iv}^{(i-1)} \geqslant$ (выполняется на шаге $i - 1$, по индукционному предположению) $\geqslant d'_{ui} + d'_{iv} \ge$ (в силу выполнения 7-ой строчки алгоритма на $i$-ой итерации и невозрастания элементов массива $d$) $\geqslant d_{uv}$. В ином случае всё очевидно: $d_{uv}^{(i)} = d_{uv}^{(i - 1)} \geqslant d'_{uv} \geqslant d_{uv}$, и неравенство тривиально. Докажем первое неравенство от противного. Пусть неравенство было нарушено, рассмотрим момент, когда оно было нарушено впервые. Пусть это была $i$-ая итерация и в этот момент изменилось значение $d_{uv}$ и выполнилось $\rho(u,v) \gt d_{uv}$. Так как $d_{uv}$ изменилось, то $d_{uv} = d_{ui} + d_{iv} \ge$ (так как ранее $\forall u, v \in V: \rho(u,v) \leqslant d_{uv}$) $\geqslant \rho(u, i) + \rho(i, v) \ge$ (по неравенству треугольника) $\geqslant \rho(u, v)$. Итак $d_{uv} \geqslant \rho(u,v)$ — противоречие.

$\triangleleft$

func floyd(w):
    d = $\omega$                // изначально $d = \omega$
    for $i \in V$
        for $u \in V$
            for $v \in V$
                d[u][v] = min(d[u][v], d[u][i] + d[i][v])

Данная реализация работает за время $\Theta(n^3)$, но требует уже $\Theta(n^2)$ памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении $\Theta$ весьма мала.

Пример работы

$i = 0$	$i = 1$	$i = 2$	$i = 3$	$i = 4$
$\begin{pmatrix} \times & 1 & 6 & \infty \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end{pmatrix}$	$\begin{pmatrix} \times & 1 & 6 & \infty \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end{pmatrix}$	$\begin{pmatrix} \times & 1 & \bf{5} & \bf{2} \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end{pmatrix}$	$\begin{pmatrix} \times & 1 & 5 & 2 \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end{pmatrix}$	$\begin{pmatrix} \times & 1 & \bf{3} & 2 \\ \infty & \times & \bf{2} & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end{pmatrix}$

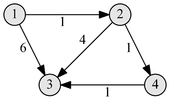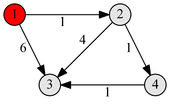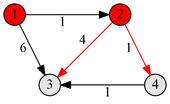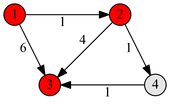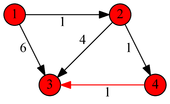
Вывод кратчайшего пути

Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив $next$, в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из $u$ в $v$ по кратчайшему пути.

Модифицированный алгоритм

func floyd(w):
    d = $\omega$               // изначально $d = \omega$
    for $i \in V$
        for $u \in V$
            for $v \in V$
                if d[u][i] + d[i][v] < d[u][v]
                    d[u][v] = d[u][i] + d[i][v]
                    next[u][v] = i

func getShortestPath(u, v):
    if d[u][v] == $\infty$
        print "No path found"                 // между вершинами u и v нет пути
    c = u
    while c != v
        print c
        c = next[c][v]
    print v

Нахождение отрицательного цикла

Утверждение:

При наличии цикла отрицательного веса в матрице $D$ появятся отрицательные числа на главной диагонали.

$\triangleright$

Так как алгоритм Флойда последовательно релаксирует расстояния между всеми парами вершин $(i, j)$, в том числе и теми, у которых $i = j$, а начальное расстояние между парой вершин $(i, i)$ равно нулю, то релаксация может произойти только при наличии вершины $k$ такой, что $d[i][k] + d[k][i] \lt 0$, что эквивалентно наличию отрицательного цикла, проходящего через вершину $i$.

$\triangleleft$

Из доказательства следует, что для поиска цикла отрицательного веса необходимо, после завершения работы алгоритма, найти вершину $i$, для которой $d[i][i] \lt 0$, и вывести кратчайший путь между парой вершин $(i, i)$. При этом стоит учитывать, что при наличии отрицательного цикла расстояния могут уменьшаться экспоненциально. Для предотвращения переполнения все вычисления стоит ограничивать снизу величиной $-\infty$, либо проверять наличие отрицательных чисел на главной диагонали во время подсчета.

Построение транзитивного замыкания

Сформулируем нашу задачу в терминах графов: рассмотрим граф $G=(V,\; E),\; |V| = n$, соответствующий отношению $R$. Тогда необходимо найти все пары вершин $(x, y)$, соединенных некоторым путем. Иными словами, требуется построить новое отношение $T$, которое будет состоять из всех пар $(x, y)$ таких, что найдется последовательность $x = x_0, x_1, \dots, x_k = y$, где $(x_{i-1}, x_i) \in R, i = 1, 2, \dots, k$.

Псевдокод

Изначально матрица $W$ заполняется соответственно отношению $R$, то есть $W[i][j] = [(i, j) \in R]$. Затем внешним циклом перебираются все элементы $k$ множества $X$ и для каждого из них, если он может использоваться, как промежуточный для соединения двух элементов $i$ и $j$, отношение $T$ расширяется добавлением в него пары $(i, j)$.

for k = 1 to n
    for i = 1 to n
        for j = 1 to n
            W[i][j] = W[i][j] or (W[i][k] and W[k][j])

Доказательство

<wikitex>Назовем промежуточной вершину некоторого пути $p = \left \langle v_0, v_1, \dots, v_k \right \rangle$, принадлежащую множеству вершин этого пути и отличающуюся от начальной и конечной вершин, то есть принадлежащую $\left \{ v_1, v_2, \dots, v_{k-1} \right \}$. Рассмотрим произвольную пару вершин $i, j \in V$ и все пути между ними, промежуточные вершины которых принадлежат множеству вершин с номерами $\left \{ 1, 2, \dots, k \right \}$. Пусть $p$ - некоторый из этих путей. Докажем по индукции (по числу промежуточных вершин в пути), что после $i$-ой итерации внешнего цикла будет верно утверждение - если в построенном графе между выбранной парой вершин есть путь, содержащий в качестве промежуточных только вершины из множества вершин с номерами $\left \{ v_1, v_2, \dots, v_{i} \right \}$, то между ними будет ребро.

• База индукции. Если у нас нет промежуточных вершин, что соответствует начальной матрице смежности, то утверждение выполнено: либо есть ребро (путь не содержит промежуточных вершин), либо его нет.
• Индуктивный переход. Пусть предположение выполнено для $i = k - 1$. Докажем, что оно верно и для $i = k$ Рассмотрим случаи (далее под вершиной будем понимать ее номер для простоты изложения):
  • $k$ не является промежуточной вершиной пути $p$. Тогда все его промежуточные пути принадлежат множеству вершин с номерами $\left \{ 1, 2, \dots, k-1 \right \} \subset \left \{ 1, 2, \dots, k \right \}$, то есть существует путь с промежуточными вершинами в исходном множестве. Это значит $W[i][j]$ будет истиной. В противном случае $W[i][j]$ будет ложью и на k-ом шаге ею и останется.
  • $k$ является промежуточной вершиной предполагаемого пути $p$. Тогда этот путь можно разбить на два пути: $i \xrightarrow{p_1} k \xrightarrow{p_2} j$. Пусть как $p_1$, так и $p_2$ существуют. Тогда они содержат в качестве промежуточных вершины из множества $\left \{ 1, 2, \dots, k-1 \right \} \subset \left \{ 1, 2, \dots, k \right \}$ (так как вершина $k$ - либо конечная, либо начальная, то она не может быть в множестве по нашему определению). Тогда $W[i][k]$ и $W[k][j]$ истинны и по индуктивному предположению посчитаны верно. Тогда и $W[i][j]$ тоже истина. Пусть какого-то пути не существует. Тогда пути $p$ тоже не может существовать, так как добраться, например, от вершины $i$ до $k$ по вершинам из множества $\left \{ 1, 2, \dots, k \right \}$ невозможно по индуктивному предположению. Тогда вся конъюнкция будет ложной, то есть такого пути нет, откуда $W[i][j]$ после итерации будет ложью.

Таким образом, после завершения внешнего цикла у нас будет $W[i][j] = true$, если между этими вершинами есть путь, содержащий в качестве промежуточных вершин из множества всех остальных вершин графа, что и есть транзитивное замыкание. </wikitex>

Оптимизация с помощью битовых масок

Строки матрицы $W$ можно хранить с помощью массива битовых маск длиной $k$. Тогда последний цикл будет выполняться в $k$ раз быстрее и сложность алгоритма снижается до $O(\frac{n^3}{k})$.
Пример реализации оптимизации с помощью битмасок:

unsigned int W[N][N / 32 + 1]
...
for k = 1 to n
    for i = 1 to n
        if бит с номером (k % 32) в маске a[i][k / 32] единичный
            for j = 1 to n
                W[i][j] = W[i][j] or W[k][j]

Источники информации

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд — М.: Издательский дом «Вильямс», 2009. — ISBN 978-5-8459-0857-5.
• Романовский И. В. Дискретный анализ: Учебное пособие для студентов, специализирующихся по прикладной математике и информатике. Изд. 3-е. — СПб.: Невский диалект, 2003. — 320 с. — ISBN 5-7940-0114-3.
• Википедия - Алгоритм Флойда — Уоршелла
• Wikipedia - Floyd–Warshall algorithm