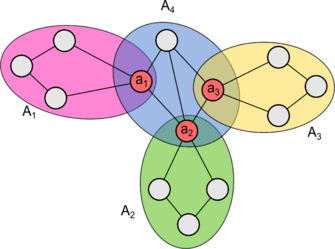
Точка сочленения, эквивалентные определения
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Определение: |
| Точка сочленения графа — вершина, принадлежащая как минимум двум блокам . |
| Определение: |
| Точка сочленения графа — вершина, при удалении которой в увеличивается число компонент связности. |
| Лемма: |
Определения и эквивалентны. |
| Доказательство: |
|
Пусть вершина принадлежит некоторым блокам и . Вершине инцидентны некоторые ребра и . Ребра и находятся в различных блоках, поэтому не существует двух непересекающихся путей между их концами. Учитывая, что один из путей между концами - путь из в эту же вершину, получаем, что любой путь, соединяющий и , пройдет через . При удалении между и не останется путей, и одна из компонент связности распадется на две.
Пусть принадлежала только одному блоку . Все вершины , смежные с , также лежат в (в силу рефлексивности отношения вершинной двусвязности). Между каждой парой вершин из существует как минимум два вершинно непересекающихся пути. Теперь удалим . Это разрушит путь , но не разрушит любой оставшийся, так как иначе он тоже прошел бы через . Рассмотрим — компоненту связности, в которой лежала . Пусть между вершинами существовал путь, проходящий через . Но он проходил также через некоторые вершины из , связность которых не нарушилась, поэтому есть как минимум еще один путь, отличный от удаленного. Противоречие: число компонент связности не увеличилось. |
| Теорема: |
Следующие утверждения эквивалентны:
|
| Доказательство: |
|
Так как — точка сочленения графа , то граф не связен и имеет по крайней мере две компоненты. Образуем разбиение , отнеся к вершины одной из этих компонент, а к — вершины всех остальных компонент. Тогда любые две вершины и лежат в разных компонентах графа . Следовательно, любой простой путь из в графа содержит . Следует из того, что (2) - частный случай (3). Если принадлежит любому простому пути в , соединяющему и , то в нет простого пути, соединяющего эти вершины в . Поскольку не связен, то — точка сочленения графа . |
| Теорема: |
Пусть — связный граф с не менее чем тремя вершинами. Следующие утверждения эквивалентны:
|
| Доказательство: |
|
Пусть , - различные вершины графа , а - множество вершин, отличных от , которые лежат на простом цикле, содержащем . Поскольку в по крайней мере три вершины и нет точек сочленения, то в нет также мостов. Значит, каждая вершина, смежная с , принадлежит , т.е. не пусто. Предположим, что не принадлежит . Пусть - вершина в , для которой расстояние (-)-цепь минимально. Пусть - кратчайшая простая (-)- цепь, а и - две простые (-)-цепи цикла, содержащего и . Так как не является точкой сочленения, то существует простая (-)-цепь , не содержащая . Обозначим через ближайшую к вершину, принадлежащую , которая также принадлежит , и через последнюю вершину (-)-подцепи в , которая принадлежит или , или . Не теряя общности, предположим, что ' принадлежит . Пусть - простая (-)-цепь, содержащая (-)-подцепь цепи и (-)-подцепь цепи , а - простая (-)-подцепь, содержащая вслед за (-')-подцепью цепи . Ясно, что и - непересекающиеся простые (-)-цепи. Вместе они образуют простой цикл, так что принадлежит . Поскольку принадлежит кратчайшей цепи, (,)<(,). Это противоречит выбору и, следовательно, доказывает, что и лежат на одном простом цикле. Следует из того, что (2) - частный случай (3). Если принадлежит любому простому пути в , соединяющему и , то в нет простого пути, соединяющего эти вершины в . Поскольку не связен, то — точка сочленения графа . |
Источники информации
- Харари, Ф. Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009