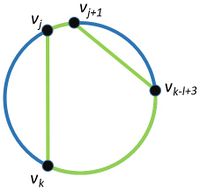
 Синим цветом выделен гамильтонов цикл. Дуги, окрашенный в зеленый цвет, образуют цикл длины l 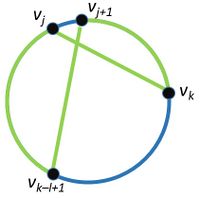 Синим цветом выделен гамильтонов цикл. Дуги, окрашенный в зеленый цвет, образуют цикл длины l Обозначим как [math] C=v_1 v_2 v_3 \ldots v_n [/math] гамильтонов цикл в графе [math] G [/math]. Для простоты расположим [math] C [/math] на окружности. Также подразумевается, что все индексы при вершинах берутся по модулю, то есть [math] v_j = v_{((j - 1)\bmod n) + 1} [/math].
Пусть в графе нет цикла длины [math] l [/math], [math] 3 \leqslant l \leqslant n-1 [/math] (по условию в графе существует гамильтонов цикл, длина которого равна [math] n [/math]). Рассмотрим две соседние вершины [math] v_j v_{j+1} [/math] и вместе с ними рассмотрим следующие пары:
Для [math]k[/math] таких, что [math] v_k [/math] лежит на дуге [math] (v_{j + l - 1}, v_{j + l}, v_{j -1}) [/math] рассмотрим пары ([math]v_j, v_k[/math]) и ([math]v_{j+1}, v_{k-l+3}[/math]) (см. рисунок слева)
Для [math]k[/math] таких, что [math] v_k [/math] лежит на дуге [math] (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) [/math] рассмотрим пары ([math]v_j, v_k[/math]) и ([math]v_{j+1}, v_{k-l+1}[/math]) (см. рисунок справа)
При добавлении таких пар ребер в графе появляется цикл длины [math] l [/math] (выделены зеленым цветом на рисунках слева и справа). Действительно:
- Рассмотрим первый случай, когда [math] v_k [/math] лежит на дуге [math] (v_{j + l - 1}, v_{j + l}, v_{j -1}) [/math] и существую ребра ([math]v_j, v_k[/math]) и ([math]v_{j+1}, v_{k-l+3}[/math]). Длина цикла равна [math] len((v_{k - l + 3}, v_{k - l + 4}, v_{k})) + 3 = k - (k - l + 3) + 3 = l - 3 + 3 = l [/math].
- Рассмотрим второй случай, когда [math] v_k [/math] лежит на дуге [math] (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) [/math] и существуют ребра ([math]v_j, v_k[/math]) и ([math]v_{j+1}, v_{k-l+1}[/math]). Тогда длина цикла равна [math] len((v_{k}, v_{k - 1}, v_{k - l + 1})) - 1 + 2 = k - (k - l + 1) - 1 + 2 = l - 1 - 1 + 2 = l [/math].
Значит в [math] G [/math] может входить максимум одно ребро из таких пар. Тогда можно утверждать, что [math] deg(v_j) + deg(v_{j + 1}) \leqslant n [/math].
Докажем методом от противного, что [math] n [/math] — четно. Пусть [math] n [/math] является нечетным, тогда из рассуждений выше существует вершина [math] v_x [/math], для которое верно, что [math] deg(v_x) \leqslant \genfrac{}{}{}{0}{n-1}{2} [/math].
Пусть это не так, тогда [math] \forall i, 1 \leqslant i \leqslant n : deg(v_i) \geqslant \genfrac{}{}{}{0}{n-1}{2} + 1 = \genfrac{}{}{}{0}{n+1}{2} [/math], значит [math] \forall j, 1 \leqslant j \leqslant n : deg(v_j) + deg(v_{j+1}) \geqslant \genfrac{}{}{}{0}{n+1}{2} + \genfrac{}{}{}{0}{n+1}{2} = n + 1 [/math], то есть мы получили противоречие с тем, что [math] deg(v_j) + deg(v_{j + 1}) \leqslant n [/math].
Без потери общности пусть [math] v_x = v_n [/math]. Рассмотрим [math] 2|E| = \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{\genfrac{}{}{}{}{n - 1}{2}} (deg(v_{2i-1}) + deg(v_{2i})) + deg(v_n) \leqslant \genfrac{}{}{}{0}{n(n-1)}{2} + [/math] [math] \genfrac{}{}{}{0}{n-1}{2} \lt \genfrac{}{}{}{0}{n^2}{2} [/math], то есть [math] |E| \lt \genfrac{}{}{}{0}{n^2}{4} [/math], но по условию [math] |E| \geqslant \genfrac{}{}{}{0}{n^2}{4} [/math] — получили противоречие. Таким образом [math] n [/math] является четным. Тогда верно, что [math] 2|E| \leqslant \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{\genfrac{}{}{}{}{n}{2}} (deg(v_{2i-1}) + deg(v_{2i})) \leqslant \genfrac{}{}{}{0}{n^2}{2} [/math], а так как по условию [math] |E| \geqslant \genfrac{}{}{}{0}{n^2}{4} [/math], то [math] |E| = \genfrac{}{}{}{0}{n^2}{4} [/math]. Данное равенство достигается, если верно, что:
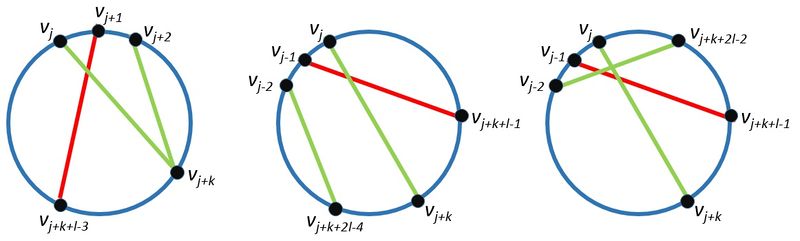 - [math] v_k [/math] лежит на дуге [math] (v_{j + l - 1}, v_{j + l}, v_{j - 1}) [/math]: [math] (v_j, v_k) \in E [/math] и [math](v_{j+1}, v_{k-l+3}) \notin E [/math]
- [math] v_k [/math] лежит на дуге [math] (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) [/math]: [math](v_j, v_k) \in E [/math] и [math](v_{j+1}, v_{k-l+1}) \notin E [/math]
Пусть [math] G [/math] не [math]K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}[/math], тогда существует такое четное число [math] k [/math], что в графе [math] G [/math] существует ребро [math] (v_j, v_{j+k}) [/math], то есть существует цикл нечетной длины. Докажем, что в таком случае существует ребро [math] (v_j, v_{j+2}) \in E [/math]. Пусть это не так и минимальное четное [math] k [/math], что [math] \exists (v_j, v_{j+k}) \in E [/math] больше двух, то есть [math] k \geqslant 4 [/math]. Тогда существует три случая:
- [math] 4 \leqslant k \leqslant n - l [/math]
[math] (v_j, v_{j+k}) \in E \Rightarrow (v_{j+1}, v_{j+k+l-3}) \notin E \Rightarrow (v_{j+2}, v_{j+k}) \in E [/math]
[math] \exists l = k-2 : (v_i, v_{i+l}) \in E [/math] — противоречие с минимальностью [math] k [/math]
- [math] n - l + 2 \leqslant k \leqslant 2n - 2l [/math]
[math] (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-4}) \in E [/math]
однако [math] 2n - k - 2l + 2 \leqslant k - 2 [/math] — противоречие с минимальностью [math] k [/math]
- [math] 2n - 2l + 2 \leqslant k \leqslant n - 2 [/math]
[math] (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-2}) \in E [/math]
однако [math] k + 2l - 2n \leqslant k - 2 [/math] — снова проиворечие с минимальностью выбранного k
Таким образом, в [math] G [/math] существует ребро [math] (v_j, v_{j+2}) [/math], но тогда [math] (v_j, v_{j+l}) \notin E [/math], а следовательно [math] (v_{j+1}, v_{j+3}) \in E [/math]. Если продолжить по всему графу, то получим, что [math] \forall j : (v_j, v_{j+2}) \in E [/math] и, как следствие, [math] G [/math] — панциклический. |


