Порождающие модели

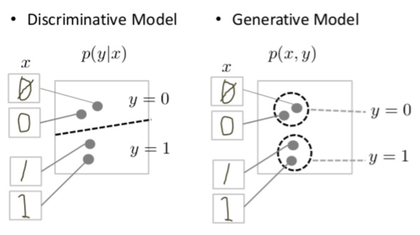
Порождающая модель пытается генерировать рукописные 0 и 1, для этого моделирует распределение по всему пространству данных. Напротив, дискриминативная модель старается разделить данные, без необходимости точно моделировать, как объекты размещаются по обе стороны от линии.

Порождающие модели (англ. generative model) — это класс моделей, которые обучают совместное распределение данных [math]p(x, y)[/math]; отсюда легко получить условное распределение [math]p(y | x)={p(x, y)\over p(x)}[/math], но совместное даёт больше информации и его можно использовать, например, для генерации новых фотографий животных, которые выглядят как настоящие животные.

С другой стороны, дискриминативная модель (англ. discriminative model) обучает только условное распределение и может, например, отличить собаку от кошки.

Классификация задачи

Можно использовать некоторые эмпирические правила для генерации новых объектов, не используя машинного обучения.

Требуется чтобы новые объекты были правдоподобными в своей области. Новое изображение человека должно быть правдоподобным, как изображение, но также человек на нём должен быть правдоподобным как человек.

Мы хотим научиться создавать правдоподобный объект относительно некоторой скрытой структуры исходных объектов. Давайте изучим распределение по ним, а затем просто будем сэмплировать новый объект из этого распределения. Значит эта задача относится к классу задач обучения без учителя.

Вычисление плотности распределения

С математической точки зрения основная цель порождающей модели обычно состоит в максимизации функции правдоподобия: для набора данных максимизировать [math]\displaystyle \prod_i p_{model}(x_i;\theta)[/math] по параметрам модели [math]\theta[/math], т.е. найти [math]\theta^* = \underset{\theta}{\operatorname{argmax}} \displaystyle \prod_i p_{model}(x_i;\theta)[/math]

Потеря порядка

Чтобы избежать арифметического переполнения снизу зачастую пользуются свойством логарифма произведения [math]\log ab = \log a+\log b[/math]. Благодаря моннотоности логарифма, его применение к обоим частям выражения не изменит параметры, при которых достигается максимум. При этом, логарифм от числа близкого к нулю будет числом отрицательным, но в абсолютном значении существенно большим чем исходное число, что делает логарифмические значения вероятностей более удобными для анализа. Что в нашем случае с вероятности очень уместно. Поэтому, мы переписываем нашу формулу с использованием логарифма.

[math]\theta^* = \underset{\theta}{\operatorname{argmax}} \log \displaystyle \prod_i p_{model}(x_i;\theta) = \underset{\theta}{\operatorname{argmax}} \displaystyle \sum_i \log p_{model}(x_i;\theta) [/math]

Важен и другой взгляд на то же самое: максимизация правдоподобия эквивалентна минимизации расстояния Кульбака-Лейблера между распределением [math]р[/math], которое получается из нашей модели, и распределением [math]\hat{p}_{data}[/math] — эмпирическим распределе­нием данных. Это эмпирическое распределение попросту полностью сосредоточе­но в точках из набора данных и равномерно распределено по ним, так что:

[math]KL(\hat{p}_{data}(x), p(x; \theta)) = \int \hat{p}_{data}(x) \log p(x; \theta) = \displaystyle \sum_i \hat{p}_{data}(x_i) \log p(x_i; \theta)[/math]

и минимизация этого выражения эквивалентна максимизации того, что выше.

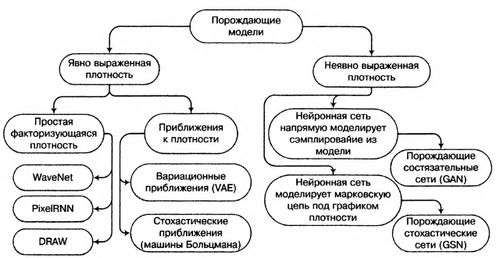
Таксономия порождающих моделей

Генеративные модели различаются как раз тем, как именно они строят рас­пределение [math]p(x; \theta)[/math]. Можно строить это распределение явно, делая вероятностные предположения, которые обычно сводятся к тому, что общее распределение [math]p(x; \theta)[/math] выражается в виде произведения тех или иных «маленьких» распределений.

Два основных подхода:

• Явный: определить распределение [math]p_{model}[/math], описывающее объекты и генерировать данные из него
• Неявный: получить некоторое распределение, оценить его близость с [math]p_{model}[/math] через дивергенцию Кульбака-Лейблера

Глубокие порождающие модели на основе нейронных сетей

• Порождающие состязательные сети
• Автокодировщик
• Вариационный автокодировщик

См. также

• Наивный байесовский классификатор(простейшая порождающая модель)

Примечания

• Примеры генерации паролей на основе исходного распределения

Источники информации

• Generative_model
• Google courses с примерами на понимание
• NIPS 2016 Tutorial: Generative Adversarial Networks(Ian Goodfellow, 2016)