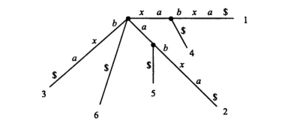
Сжатое суффиксное дерево

Определение:

Пусть дана строка [math]s[/math], [math]|s| = m[/math]. Суффиксное дерево [math]T[/math] для строки [math]s[/math] - ориентированное дерево с корнем, имеющее ровно [math]m[/math] листьев, занумерованных от [math]1[/math] до [math]m[/math]. Каждая внутренняя вершина, отличная от корня, имеет не меньше двух детей, а каждая дуга помечена непустой подстрокой строки [math]s[/math]. Никакие две дуги не могут иметь пометок, начинающихся с одного и того же символа.

Главная особенность суффиксного дерева заключается в том, что для каждого листа [math]i[/math] конкатенация меток дуг на пути от корня к листу [math]i[/math] в точности составляет суффикс строки [math]s[/math], который начинается в позиции [math]i[/math], то есть [math]s[i..m][/math].

Существование сжатого суффиксного дерева

Суффиксный бор для строки [math]xabxa[/math] с защитным символом

Определение суффиксного дерева не гарантирует, что такое дерево существует для любой строки [math]s[/math]. Если один суффикс совпадает с префиксом другого суффикса, то построить суффиксное дерево, удовлетворяющее данному выше определению, невозможно, поскольку путь для первого суффикса не сможет закончиться в листе. Например, для строки [math]xabxa[/math] суффикс [math]xa[/math] является префиксом суффикса [math]xabxa[/math]. Во избежание этого в конце строки [math]s[/math] добавляется символ, не входящий в исходный алфавит. Такой символ называется защитным. Как правило в качестве защитного символа используется [math]\$[/math].

Связь с суффиксным бором

Пусть [math]P[/math] - суффиксный бор строки [math]s[/math]. Тогда сжатое суффиксное дерево [math]T[/math] может быть получено из [math]P[/math] слиянием каждого пути из неветвящихся вершин в одну дугу.