Эта статья находится в разработке!
Как обычно, будем рассматривать функцию двух переменных.
[Тут какое-то невнятно написанное предложение про мотивацию]
Площадь сектора [math]S = \frac12R^2\alpha[/math]. Пусть эта формула нам известна. (рис 1)
КАРТИНКА КАРТИНКА
[math]\Delta \alpha[/math], [math]\Delta r \approx 0[/math]
[math]\Delta S = \frac12(r + \Delta r)^2\Delta \alpha - \frac12r^2\Delta \alpha[/math]
[math]=\frac12\Delta\alpha(2r + \Delta r) \Delta r[/math]
[math]=r\Delta\alpha \Delta r + \frac12\Delta \alpha(\Delta r)^2[/math]
[math]\frac{\Delta S}{\Delta\alpha\Delta r} = r + \frac12\Delta r[/math]
[math]\Delta \alpha, \Delta r \to 0 \Rightarrow \frac{\Delta S}{\Delta\alpha \Delta r} \to 0[/math]
Или, [math]\Delta S \approx r\Delta\alpha\Delta r[/math].
Рассмотрим полярные координаты. [math]\begin{cases}x & = r\cos \alpha\\y & = r\sin\alpha\end{cases}[/math]
Рассмотрим линии уровня. [math]l_r[/math] — ГМТ, для каждой из которых значение радиуса одно и то же и равно [math]r[/math].
Аналогично, [math]l_\alpha[/math] — ГМТ, для каждой из которых [math]\alpha = \mathrm{const}[/math]
Меняя в [math]l_r[/math] и [math]l_\alpha[/math] [math]r[/math] и [math]\alpha[/math], покрываем плоскость сетью окружностей и лучей.
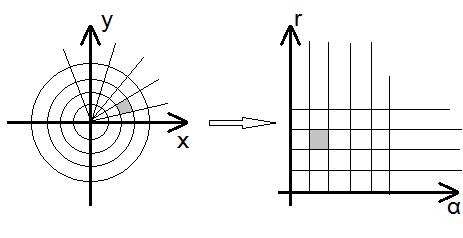
Если на написанную систему соотношений смотреть как на преобразование плоскости и смотреть образы [math]l_r[/math] и [math]l_\alpha[/math],
в силу их определений это будет сеть вертикалей и горизонталей.
Если заштриховать фигуру, границы которой — эти линии, то её образ будет прямоугольником. При обозначении его площади за [math]\Delta S[/math] получаем
предел выше. Тогда этот предел — коэффициент искажения элементарной площади при переходе из одной системы осей в другую.
[math]T(\alpha, r) = \binom{x=r\cos\alpha}y=r\sin\alpha[/math]
Прямоугольник [math]\Delta\alpha\times\Delta r[/math] под действим [math]T[/math] переходит в [math]\Delta S[/math], причём [math]\frac{\Delta S}{\Delta\alpha\Delta r} \to r[/math]([math]\Delta\alpha, \Delta r \to 0[/math]).
Итак, первый этап завершён. Найдена плотность(коэффициент искажения).
На втором этапе мы заинтегрируем эту плотность и придём к формуле [math]|E| = \iint\limits_E dxdy = \iint\limits_{E'} rd\alpha dr[/math], которая будет
базовой формулой для того, что бы научиться заменять переменные в двойных интегралах.
Будем считать, что мы знаем, что если есть [math]P \in E_P[/math], [math]E'_P[/math] — образ, то
[math]\frac{E_P}{E'_P} \xrightarrow[\operatorname{diam} E_P \to 0]{} r[/math], где [math]P =(x, y) = (\alpha, r)[/math]. Это стремление равномерно по положению точки в
пределах прямоугольника. (рис 5)
КАРТИНКА
[math]\forall\varepsilon \gt 0\ \exists \delta \gt 0 : \operatorname{diam} E_P \lt \delta \Rightarrow \left|\frac{|E_p|}{|E'_P|} - r \right| \lt \varepsilon[/math]
Рассмотрим квадрируемую фигуру [math]E[/math]. [math]E = \bigcup\limits_{j = 1}^p E_j[/math], [math]|E| = \sum\limits_{j = 1}^p |E_j|[/math]
[math]|E_j| = r_j|E'_j| + \alpha_j |E'_j|[/math], где [math]\alpha_j[/math] — бесконечно малое.
[math]|E| = \sum\limits_{j = 1}^p r_j |E'_j| + \sum\limits_{j = 1}^p \alpha_j |E'_j|[/math]
По равномерной непрерывности, при [math]\operatorname{diam} E'_j \lt \delta[/math], [math]\sum\limits_{j=1}^p\alpha_j|E'_j| \leq \varepsilon\sum\limits_{j = 1}^p|E'_j|[/math].
Тогда первое слагаемое — интегральная сумма, а второе стремится к нулю. Тогда
[math]E = \iint\limits_{E'}rd\alpha dr + 0 = \iint\limits_{E'} rd\alpha dr[/math]
Пример.
КАРТИНКА
Плошадь круга. [math]|E| = \iint\limits_\Pi r d\alpha dr[/math] [math]= \int\limits_0^{2\pi} d\alpha \int\limits_0^R r dr[/math] [math]=\pi r^2[/math]
