Эргодическая марковская цепь

Определение:

Марковская цепь называется эргодической, если существует дискретное распределение (называемое эргодическим) [math]\pi = (\pi_1,\pi_2,\ldots )^{\top}[/math], такое что [math]\pi_i \gt 0,\; i \in \mathbb{N}[/math] и [math]\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, \quad \forall i=1,2, \ldots[/math].

Определение:

Марковская цепь называется эргодической, если любое состояние цепи является эргодическим (состояние цепи Маркова эргодическим, если оно одновременно возвратно и непериодично).

Пример

Пример эргодической цепи

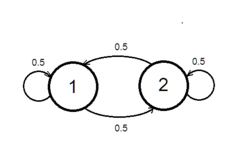
Рассмотрим эксперимент по бросанию честной монеты. Тогда соответствующая этому эксперименту марковская цепь будет иметь 2 состояния. Рассмотрим матрицу, следующего вида: [math]p_{ij}=0.5, i,j=1,2[/math].

Такая матрица является стохастической, а, значит, корректно определяет марковскую цепь. Такая цепь является эргодической, так как существует эргодическое распределение [math]\pi = (0.5,0.5)^{\top}[/math], такое что [math]\lim\limits_{n \to \infty} p_{ij}^{(n)} = \pi_j, i=1,2[/math].

См. также

• Марковская цепь

• Регулярная марковская цепь

Ссылки

• Эргодическое распределение - Википедия

• Дискретное распределение - Википедия

Литература

Дж. Кемени, Дж. Снелл "Конечные цепи Маркова"