Генерация комбинаторных объектов в лексикографическом порядке
Определение
Генерация комбинаторных объектов в лексикографическом порядке — непосредственное построение и перебор всех объектов заданного типа так, чтобы для любых двух объектов выполнялось условие: .
Алгоритм построения
Описание процедуры построения
Данный алгоритм генерирует все объекты заданного типа в лексикографическом порядке. На каждом шаге генерируется минимальный возможный префикс требуемого объекта.
Пусть — процедура генерирования, где — глубина рекурсии, — комбинаторный объект.
Gen(K, p)
if p = <требуемый размер объекта>
<выводим> K
else
for <все w из алфавита на котором строится K>
if (K + w) = <корректный префикс требуемого объекта>
Gen(K + w, p + 1)
Генерация с помощью процедуры получения следующего объекта
Составляем первый объект — , для него получаем следующий объект — , для получаем , далее действуем также, для получая объект, пока не получим последний объект .
Примеры
Пример генерации сочетаний из N элементов по M в лексикографическом порядке
Пусть — процедура генерирования, где — текущее сочетание, — следующий элемент в сочетании, — глубина рекурсии.
procedure gen(k, l);
begin
a[l] = k;
if l = m then <проверка на требуемый размер объекта>
begin
for j = 1 to m do write(a[j], ' '); <вывод объекта>
writeln;
end else for i = k + 1 to n do rec(i, l + 1); <>
end;
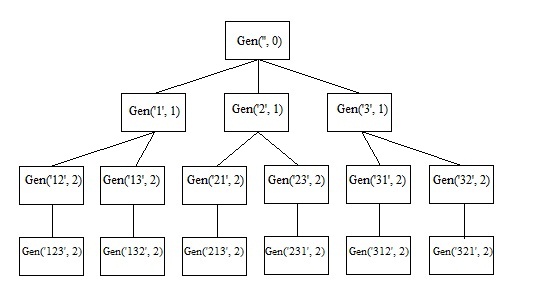
Пример работы процедуры генерации
Иллюстрация работы процедуры генерирования всех перестановок из чисел