Интерактивные протоколы. Класс IP. Класс AM

Класс IP

Определение:

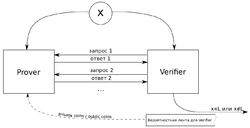
Интерактивным протоколом, разрешающим язык [math]L[/math], называется абстрактная машина (см. рис. 1), моделирующая вычисления как обмен сообщениями между двумя программами ([math]Prover[/math] и [math]Verifier[/math], далее [math]P[/math] и [math]V[/math] соответственно), такими, что [math]P[/math] убеждает [math]V[/math] в том, что слово [math]x[/math] принадлежит языку; [math]P[/math] не ограничен в вычислительной мощности; [math]V[/math] — вероятностная машина Тьюринга; [math]V[/math] ограничен полиномиальным временем работы.

Рис. 1. Схема интерактивного протокола.

Интерактивные протоколы делятся на два типа в зависимости от доступа [math]P[/math] к вероятностной ленте [math]V[/math]:

1. public coins — [math]P[/math] может видеть вероятностную ленту [math]V[/math];
2. private coins — [math]P[/math] не может видеть вероятностную ленту [math]V[/math].

Определение:

[math]IP[f] = \{L|\exists \langle V, P \rangle : [/math] [math] \forall x \in L \Rightarrow P(V(x) = 1) \ge \frac{2}{3} [/math] [math] \forall x \notin L \Rightarrow P(V(x) = 1) \le \frac{1}{3} [/math] число раундов интерактивного протокола [math] O(f(n)), n = |x| [/math]

Определение:

Если для интерактивного протокола выполняется [math] \forall x \in L \Rightarrow P(V(x) = 1) = 1 [/math], то говорят, что он обладает свойством completeness (его можно достичь).

Определение:

Если для интерактивного протокола выполняется [math] \forall x \notin L \Rightarrow P(V(x) = 1) = 0 [/math], то говорят, что он обладает свойством soundness (его нельзя достичь).

Теорема:

[math]\mathrm{BPP} \subset \mathrm{IP[0]}[/math]

Доказательство:

[math]\triangleright[/math]

Это очевидным образом следует из определений [math]\mathrm{BPP}[/math] и [math]V[/math] в [math]\mathrm{IP}[/math]; [math]V[/math] даже не требуется общаться с [math]P[/math].

[math]\triangleleft[/math]

Теорема:

[math]\mathrm{NP} \subset \mathrm{IP[1]}[/math]

Доказательство:

[math]\triangleright[/math]

[math]V[/math] будет проверять на принадлежность слова [math]x[/math] используя сертификат, который он запросит у [math]P[/math]. Так как [math]P[/math] неограничен в вычислительной мощности, он может подобрать подходящий сертификат и именно его и сообщит, так как он заинтересован в том, чтобы [math]V[/math] принял слово. Для этого требуется лишь один раунд интерактивного протокола, что и доказывает теорему.

[math]\triangleleft[/math]