Интерактивные протоколы. Класс IP. Класс AM

Определения

Определение:

Интерактивным протоколом, разрешающим язык [math]L[/math], называется абстрактная машина (см. рисунок), моделирующая вычисления как обмен сообщениями между двумя программами ([math]\mathit{Prover}[/math] и [math]\mathit{Verifier}[/math]), такими, что [math]\mathit{Prover}[/math] заинтересован в том, чтобы [math]\mathit{Verifier}[/math] решил, что слово [math]x[/math] принадлежит языку; [math]\mathit{Prover}[/math] не ограничен в вычислительной мощности; [math]\mathit{Verifier}[/math] заинтересован установить, действительно ли слово [math]x[/math] принадлежит языку; [math]\mathit{Verifier}[/math] — вероятностная машина Тьюринга; [math]\mathit{Verifier}[/math] ограничен полиномиальным временем работы.

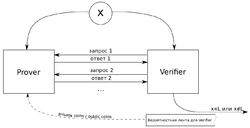
Схема интерактивного протокола.

[math]\mathit{Verifier}[/math], обменивающийся сообщениями с [math]\mathit{Prover}[/math], будем обозначать [math]\mathit{Verifier^{Prover}}[/math].

Интерактивные протоколы делятся на два типа в зависимости от доступа [math]\mathit{Prover}[/math] к вероятностной ленте [math]\mathit{Verifier}[/math]:

1. public coins — [math]\mathit{Prover}[/math] может видеть вероятностную ленту [math]\mathit{Verifier}[/math];
2. private coins — [math]\mathit{Prover}[/math] не может видеть вероятностную ленту [math]\mathit{Verifier}[/math].

Определение:

[math]\mathrm{IP}[f] = \{L\bigm|\exists \langle \mathit{Verifier}, \mathit{Prover} \rangle : [/math] [math]\mathit{Prover}[/math] не имеет доступа к вероятностной ленте [math]\mathit{Verifier}[/math] (private coins); [math] \forall x \in L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \ge \frac{2}{3} [/math]; [math] \forall x \notin L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \le \frac{1}{3} [/math]; число раундов интерактивного протокола [math] O(f(n)), n = |x|\}[/math].

Определение:

[math]\mathrm{IP}=\bigcup\limits_{p(n) \in poly} \mathrm{IP} [p(n)] [/math]

Язык [math]\mathrm{AM}[/math] (Arthur–Merlin games) отличается от [math]\mathrm{IP}[/math] лишь тем, что [math]\mathit{Prover}[/math] может видеть вероятностную ленту [math]\mathit{Verifier}[/math].

Определение:

[math]\mathrm{AM}[f] = \{L\bigm|\exists \langle \mathit{Verifier}, \mathit{Prover} \rangle : [/math] [math]\mathit{Prover}[/math] может читать вероятностную ленту [math]\mathit{Verifier}[/math] (public coins); [math] \forall x \in L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \ge \frac{2}{3} [/math]; [math] \forall x \notin L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) \le \frac{1}{3} [/math]; число раундов интерактивного протокола [math] O(f(n)), n = |x|\} [/math].

Определение:

[math]\mathrm{AM}=\bigcup\limits_{p(n) \in poly} \mathrm{AM} [p(n)] [/math]

Определение:

Если для интерактивного протокола выполняется [math] \forall x \in L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) = 1 [/math], то говорят, что он обладает свойством completeness .

Определение:

Если для интерактивного протокола выполняется [math] \forall x \notin L \Rightarrow P(\mathit{Verifier^{Prover}}(x) = 1) = 0 [/math], то говорят, что он обладает свойством soundness .

Свойство completeness можно достичь, а soundness достичь нельзя.