Эквивалентность состояний ДКА

Эквивалентность автоматов

• Определение: Два автомата [math]\mathcal{A}_1(Q_1,\Sigma,\delta_1,s_10, T_1\subseteq Q_1)[/math] и [math]\mathcal{A}_2(Q_2,\Sigma,\delta_2,s_20, T_2\subseteq Q_2)[/math] называются эквивалентными, если они распознают один и тот же язык над алфавитом [math]\Sigma[/math].
• Определение: Два состояния [math]s_i[/math] и [math]s_j[/math] называются эквивалентными [math](s_i \sim s_j)[/math], если [math]\forall z\in \Sigma^*[/math] верно, что [math]\delta(s_i, z)\in T \Leftrightarrow \delta(s_j, z)\in T[/math]. Из этого следует, что если два состояния [math]s_i[/math] и [math]s_j[/math] эквивалентны, то и состояния [math]\delta_1(s_i, a)[/math] и [math]\delta_2(s_j, a)[/math] будут эквивалентными для [math]\forall a \in \Sigma[/math]. Кроме того, т.к. переход [math]\delta(s, \varepsilon)[/math] может возникнуть только для конечного состояния [math]s[/math], то никакое допускающее(терминальное) состояние не может быть эквивалентно не допускающему состоянию. Нахождение классов эквивалентных состояний внутри автомата и их совмещение в одно состояние используется в быстром алгоритме Хопкрофта для минимизации автомата, работающий за [math]O(n \log n)[/math].
• Определение: Слово [math]z \in \Sigma^*[/math] различает два состояния [math](s_i \nsim s_j)[/math], если [math]\delta(s_i, z)\in T \Leftrightarrow \delta(s_j, z)\notin T[/math]. Также, если слово [math]z[/math] различает состояния [math]t_1[/math] и [math]t_2[/math] такие, что [math]t_1=\delta(q_1, a)[/math] и [math]t_2=\delta(q_2, a)[/math], то слово [math]aw[/math] различает состояния [math]q_1[/math] и [math]q_2[/math]. Нахождение пар различных состояний в автомате используется в алгоритме минимизации автомата, работающий за [math]O(n^2)[/math].

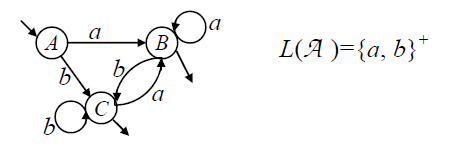
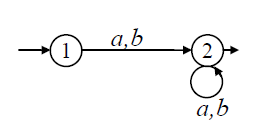
• Пример двух эквивалентных автоматов: