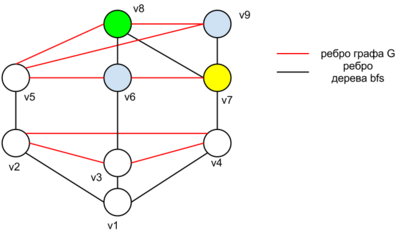
|
Для доказательства теоремы рассмотрим несколько случаев:
- [math]\Delta(G) \le 2[/math], тогда:
- Если [math] \Delta = 0[/math], [math] G = K_1[/math]
- Если [math] \Delta = 1[/math], [math] G = K_2[/math]
- Если [math] \Delta = 2[/math], то:
- [math] G [/math]— либо дерево либо четный цикл и тогда [math] \chi(G) = 2[/math]
- [math] G[/math] нечетный цикл
- [math]\Delta(G) \ge 3[/math], тогда:
- Если [math]G[/math] не является вершинно двусвязным графом, тогда в графе [math] G[/math] [math] \exists[/math] [math] v \in V[/math] — точка сочленения. Пусть [math]G_1,G_2[/math] — две компоненты связности, полученные при удалении вершины [math]v[/math].Тогда, по выше доказанной лемме [math]G_1,G_2[/math] можно правильно раскрасить в не более чем [math]\Delta[/math] цветов.Поскольку количество соседей вершины [math] v [/math] в каждой из компонент не более [math] \Delta - 1[/math], то [math]G[/math] можно правильно раскрасить в не более чем [math]\Delta[/math] цветов.
- Если [math]G[/math] является вершинно двусвязным графом. Тогда, [math] \exists[/math] [math] v,u \in V :(u,v) \notin E[/math] и при удалении вершин [math]v,u[/math] граф теряет связность .Пусть [math]G_1,G_2[/math] — два подграфа [math] G:(G_1 \cap G_2 = \{v,u\}) \land (G_1 \cup G_2 = G)[/math]. Рассмотрим два случая.
- Если сумма степеней вершин [math]u,v[/math] в каждом из подграфов [math]G_1,G_2[/math] меньше [math]2(\Delta-1)[/math]. Тогда, в одном из подграфов [math] G_1,G_2[/math] [math] deg\ u \le \Delta - 2 [/math] или [math] deg\ v \le \Delta - 2 [/math].Тоесть, подграфы [math]G_1,G_2[/math] можно правильно раскрасить в не более чем [math]\Delta[/math] цветов так, чтобы вершины [math] u,v [/math] были бы разных цветов.А из этого следует, что граф [math]G[/math] тоже можно правильно раскрасить в не более чем [math]\Delta[/math] цветов.
- Если сумма степеней вершин [math]u,v[/math] в одном из подграфов [math]G_1,G_2[/math] равна [math]2(\Delta-1)[/math].Тогда, степени обоих вершин в одном из подграфов равны [math] \Delta - 1[/math], например, в подграфе [math]G_1[/math]:
- Если вершины [math]u,v[/math] смежны с вершиной [math]p \in G_2[/math], тогда мы можем правильно раскрасить [math]G_2[/math], где степени вершин [math]u,v[/math] равны [math]1[/math], в не более чем [math] \Delta [/math] цветов так, чтобы вершины [math]u,v[/math] были одного цвета. Следовательно, можно покрасить граф [math]G[/math] в не более чем [math]\Delta[/math] цветов.
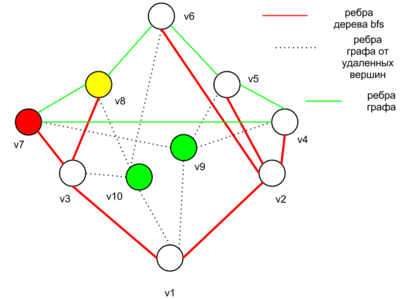 Алгоритм раскраски. Третий случай, пятый шаг
- Если [math]G[/math] является [math]k[/math]-связным графом, где [math]k \gt 2[/math]. Тогда, рассмотрим [math]w \in V : deg\ w = \Delta[/math]. У вершины [math]w[/math] должны существовать две соседние вершины [math]u,v : uv \notin E [/math], в противном случае [math]G = K_n[/math].Пусть [math]G_- = G - u - v [/math]. Заметим, что [math]G_-[/math] связный граф, запустим для [math]G_-[/math] алгоритм обхода в ширину из вершины [math]w[/math]. Пронумеруем вершины [math]v_1,...,v_{n-2}[/math], где [math]v_i[/math] вершина рассмотренная на [math]i[/math]ом шаге алгоритма bfs.Теперь пусть [math] v_{n-1} = v[/math],и [math]v_n = u[/math]. Покрасим [math]v_n,v_{n-1}[/math] в один цвет, далее начнем красить вершины в обратном порядке, начиная с [math]v_{n-2}[/math] в один из [math]\Delta[/math] цветов так, чтобы никакое ребро графа не соединяло вершины одного цвета. Заметим, что так всегда можно сделать, поскольку на [math] i[/math]ом шаге покраски, где [math]i \neq n[/math], для вершины [math] v_{n - i+1}[/math] есть не более [math]\Delta(G) - 1[/math] уже покрашенных соседей, следовательно, вершину [math] v_{n-i+1}[/math] можно покрасить по крайней мере в один из свободных цветов. Вершину [math]w[/math] мы тоже сможем правильно раскрасить в один из [math]\Delta[/math] цветов потому, что ее [math]\Delta[/math] соседей покрашено в не более чем [math]\Delta - 1[/math] цветов. Таким образом граф [math] G[/math] можно правильно раскрасить в не более чем [math]\Delta[/math] цветов.
|