Замкнутость КС-языков относительно различных операций

В отличие от регулярных языков, КС-языки не замкнуты относительно всех теоретико-множественных операций. К примеру, дополнение и пересечение КС-языков не обязательно являются КС-языками.

Здесь и далее считаем, что [math] L_1 [/math] и [math] L_2 [/math] — КС языки.

Операции с КС-языками

Объединение

Утверждение:

[math] L_1 \cup L_2 [/math] также является КС-языком.

[math]\triangleright[/math]

Построим КС-грамматику для языка [math] L_1 \cup L_2 [/math]. Для этого рассмотрим соответствующие КС-грамматики для языков [math] L_1 [/math] и [math] L_2 [/math]. Пусть стартовые символы в них имеют имена [math] S [/math] и [math] T [/math] соответственно. Тогда стартовый символ для [math] L_1 \cup L_2 [/math] обозначим за [math] S' [/math] и добавим правило [math] S' \to S\,|\,T [/math]. Покажем, что [math] S' \Rightarrow^{*} w \iff S \Rightarrow^{*} w \lor T \Rightarrow^{*} w [/math]. В левую сторону: поскольку [math] S \Rightarrow^{*} w [/math] и есть правило [math] S' \to S [/math], то, по определению [math] \Rightarrow^{*} [/math] получаем, что [math] S' \Rightarrow^{*} w [/math]. Аналогично и для [math] T [/math]. В обратную сторону, пусть [math] S' \Rightarrow^{*} w [/math]. Поскольку [math] S' \to S\,|\,T [/math] — единственные правила, в которых нетерминал [math] S' [/math] присутствует в правой части, то это означает, что либо [math] S' \Rightarrow S \Rightarrow^{*} w [/math], либо [math] S' \Rightarrow T \Rightarrow^{*} w [/math], что и требовалось доказать.

[math]\triangleleft[/math]

Конкатенация

Утверждение:

[math] L_1 \cdot L_2 [/math] — КС-язык.

[math]\triangleright[/math]

Аналогично предыдущему случаю построим КС-грамматику для языка [math] L_1 \cdot L_2 [/math]. Для этого добавим правило [math] S' \to S T [/math], где [math] S [/math] и [math] T [/math] — стартовые символы языков [math] L_1 [/math] и [math] L_2 [/math] соответственно. Остальное доказательство аналогично случаю с объединением.

[math]\triangleleft[/math]

Замыкание Клини

Утверждение:

[math] L^{*} = \bigcup\limits_{i = 0}^{\infty} L^i [/math] — КС-язык.

[math]\triangleright[/math]

Если [math] S [/math] — стартовый символ КС-грамматики для языка [math] L [/math], то добавим в КС-грамматику для языка [math] L^{*} [/math] новый стартовый символ [math] S' [/math] и правила [math] S' \to S S' \, | \, \varepsilon [/math].

[math]\triangleleft[/math]

Прямой и обратный гомоморфизм

В случае с прямым гомоморфизмом всё просто: строится КС-грамматика, в которой каждый символ [math] x \in \Sigma [/math] заменяется на [math] h(x) [/math].

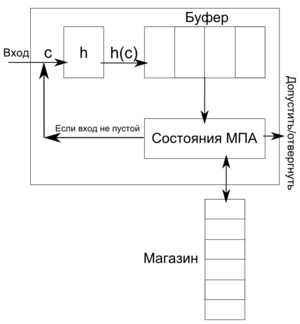
Для доказательства замкнутости обратного гомоморфизма будем делать аналогично доказательству для регулярных языков. Построим МП-автомат для [math] h^{-1}(L) = \{ w \mid h(w) \in L \} [/math] на основе МП-автомата для языка [math] L [/math] (назовем его [math] M [/math]). Новый автомат [math] M' [/math] будет действовать следующим образом:

1. Если входное слово закончилось, допускаем или не допускаем его по допускающему состоянию.
2. Иначе считываем символ [math] c [/math].
3. Сохраняем [math] h(c) [/math] в буфере.
4. Запускаем [math] M [/math] на слове, находящемся в буфере.
5. После того, как [math] M [/math] обработал весь буфер, переходим к пункту 2.

Если рассмотреть более формально, пусть [math] M =\langle Q, \Sigma, \Gamma, \delta, s, Z_{0}, T\rangle [/math], тогда [math] M' =\langle Q', \Sigma, \Gamma, \delta', (s, \varepsilon), Z_{0}, T \times {\varepsilon}\rangle[/math].

• [math] Q' = \{ (q, x) \mid q \in Q \} [/math], где [math] x [/math] — суффикс (не обязательно собственный) некоторой цепочки [math] h(c) [/math] для символа [math] c \in \Sigma [/math]. Таким образом, первый компонент состояния [math] M' [/math] является состоянием [math] M [/math], а второй — компонентом буфера.
• [math] \delta' [/math] определяется следующими правилами:
  • [math] \delta'((q, \varepsilon), c, X) = \{((q, h(c)), X) \mid c \in \Sigma, q \in Q, X \in \Gamma \}[/math]. Когда буфер пуст, [math] M' [/math] может прочитать свой следующий входной символ [math] c [/math] и поместить [math] h(c) [/math] в буфер.
  • Если [math] (p, \gamma) \in \delta(q, b, X), b \in T \cup \varepsilon [/math], то [math] ((p, x), \gamma) \in \delta'((q, bx), \varepsilon, X) [/math]. Таким образом, [math] M' [/math] всегда имеет возможность имитации перехода [math] M [/math], используя голову буфера. Если [math] b \in T [/math], то буфер должен быть непустым, но если [math] b = \varepsilon [/math], то буфер может быть пустым.
• Начальным состоянием [math] M' [/math] является [math] (s, \varepsilon) [/math], т.е. [math] M' [/math] стартует в начальном состоянии [math] M [/math] с пустым буфером.
• Допускающими состояниями [math] M' [/math] являются состояния [math] (q, \varepsilon)[/math], где [math] q \in T [/math].

Таким образом получаем, что [math](s, h(w), Z_0) \vdash_M^{*} (p, \varepsilon, \gamma) \Leftrightarrow ((s, \varepsilon), w, Z_0) \vdash_{M'}^{*} ((p, \varepsilon), \varepsilon, \gamma)[/math], то есть автомат [math] M' [/math] допускает те и только те слова, которые принадлежат языку [math] h^{-1}(L) [/math].

Разворот

Для того, чтобы построить КС-грамматику для языка [math] L^{R} = \{ w^{R} \mid w \in L \} [/math], необходимо развернуть все правые части правил грамматики для [math] L [/math].

Покажем, что [math]w \in L \Rightarrow w^{R} \in L^{R}[/math]. Докажем индукцией по длине порождения в грамматике [math]L[/math].

База. [math]A \underset{L}{\Rightarrow} w[/math].

В грамматике [math]L[/math] существует правило [math]A \rightarrow w[/math] и, так как мы развернули все правые части правил, то [math]A \underset{L^{R}}{\Rightarrow} w^{R}[/math].

Предположение индукции. Пусть [math]A \underset{L}{\Rightarrow}^* w[/math] менее чем за [math]n[/math] шагов, тогда [math]A \underset{L^{R}}{\Rightarrow}^* w^{R}[/math].

Переход. Пусть в порождении [math]n[/math] шагов, [math]n \gt 1[/math]. Тогда оно имеет вид [math]A \underset{L}{\Rightarrow}Y_1 Y_2...Y_m \underset{L}{\Rightarrow}^*w[/math], где [math] Y_i \in N \cup \Sigma [/math]. Цепочку [math] w [/math] можно разбить на [math]w_1 w_2...w_m[/math], где [math] Y_i \underset{L}{\Rightarrow}^*w_i[/math]. Так как каждое из порождений [math] Y_i \underset{L}{\Rightarrow}^*w_i [/math] содержит менее [math] n [/math] шагов, к ним можно применить предположение индукции и заключить, что [math] Y_i \underset{L^{R}}{\Rightarrow}^*w_i^{R} [/math]. Так как [math]A \underset{L}{\Rightarrow}Y_1 Y_2...Y_m[/math], то [math]A \underset{L^{R}}{\Rightarrow}Y_m Y_{m - 1}...Y_1[/math], откуда следует, что [math] A \underset{L^{R}}{\Rightarrow}^* w^{R} [/math].

Дополнение, пересечение и разность

В отличие от регулярных языков, дополнение до КС-языка, пересечение КС-языков и разность КС-языков может не быть КС-языком.

Утверждение:

[math] L = \{ww \mid w \in \Sigma^{*} \} [/math] не является КС-языком, однако [math] \overline{L} [/math] — КС-язык.

[math]\triangleright[/math]

То, что [math] L [/math] — не КС язык, доказывается с помощью леммы о разрастании. Для [math] \overline{L} [/math] можно составить КС-грамматику.

[math]\triangleleft[/math]

Утверждение:

Если [math] L_1 = a^i b^i c^j , L_2 = a^i b^j c^j [/math], то [math] L_1 \cap L_2 [/math] не является КС-языком.

[math]\triangleright[/math]

[math] L_1 = \{ a^i b^i \} \cdot \{ c^j \}, L_2 = \{ a^i \} \cdot \{ b^j c^j \} [/math]. По замкнутости КС-языков относительно конкатенации получаем, что [math] L_1 [/math] и [math] L_2 [/math] являются КС-языками. Но [math] L_1 \cap L_2 = \{ a^i b^i c^i \mid i \in \mathbb{N} \} [/math], что по лемме о разрастании для КС-языков не является КС-языком.

[math]\triangleleft[/math]

Для разности достаточно заметить, что [math] \overline{L} = \Sigma^{*} \setminus L [/math], поэтому разность КС-языков также необязательно является КС-языком.

Более того, задачи определения того, является ли дополнение КС-языка КС-языком и проверки непустоты пересечения КС-языков являются алгоритмически неразрешимыми.

Примеры других операций

Определение:

[math] \mathrm{Half}(L) = \{ w \mid ww \in L \} [/math]

Операция [math] \mathrm{Half} [/math] также не сохраняет КС-язык таковым. Рассмотрим язык [math] L = \{ a^n b a^n b a^m b a^l b a^k b a^k b \} [/math]. [math] L [/math] — КС-язык. Посмотрим, что есть [math] \mathrm{Half}(L) [/math]. Пусть [math] \alpha = a^n b a^n b a^m b a^l b a^k b a^k b = ww [/math]. Отсюда следует, что:

• [math] n = l [/math]
• [math] n = k [/math]
• [math] m = k [/math]

А значит, [math] n = l = k = m [/math], и [math] \mathrm{Half}(L) = \{ a^n b a^n b a^n b \} [/math], и по лемме о разрастании КС-языком не является.

Операции над КС-языком и регулярным языком

Пересечение

Тем не менее, хоть пересечение двух КС-языков не обязательно является КС-языком, но пересечение КС-языка и регулярного языка — всегда КС-язык. Для доказательства этого построим МП-автомат для пересечения регулярного языка и КС-языка.

Пусть регулярный язык задан своим ДКА, а КС-язык — своим МП-автоматом c допуском по допускающему состоянию. Построим прямое произведение этих автоматов так же, как строилось прямое произведение для двух ДКА.

Более формально, пусть [math] R [/math] — регулярный язык, заданный своим ДКА [math] \langle \Sigma, Q_1, s_1, T_1, \delta_1 \rangle [/math], и [math] L [/math] — КС-язык, заданный своим МП-автоматом: [math] \langle \Sigma, \Gamma, Q_2, s_2, T_2, z_0, \delta_2 \rangle [/math]. Тогда прямым произведением назовем следующий автомат:

• [math] Q = \{ \langle q_1, q_2 \rangle \mid q_1 \in Q_1, q_2 \in Q_2 \} [/math]. Иначе говоря, состояние в новом автомате — пара из состояния первого автомата и состояния второго автомата.
• [math] s = \langle s_1, s_2 \rangle [/math]
• Стековый алфавит [math] \Gamma [/math] остается неизменным.
• [math] T = \{ \langle t_1, t_2 \rangle \mid t_1 \in T_1, t_2 \in T_2 \} [/math]. Допускающие состояния нового автомата — пары состояний, где оба состояния были допускающими в своем автомате.
• [math] \delta ( \langle q_1, q_2 \rangle, c, d) = \langle \delta_1 (q_1, c), \delta_2 (q_2, c, d) \rangle [/math]. При этом на стек кладется то, что положил бы изначальный МП-автомат при совершении перехода из состояния [math] q_2 [/math],

видя на ленте символ [math] c [/math] и символ [math] d [/math] на вершине стека.

Этот автомат использует в качестве состояний пары из двух состояний каждого автомата, а за операции со стеком отвечает только МП-автомат. Слово допускается этим автоматом [math] \iff [/math] слово допускается и ДКА и МП-автоматом, то есть язык данного автомата совпадает с [math] R \cap L [/math].

Разность

Разность КС-языка и регулярного языка выражается следующим образом: [math] L \setminus R = L \cap \overline{R} [/math], а, поскольку регулярные языки замкнуты относительно дополнения, то разность можно выразить через пересечение.

Литература

• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — C. 302-304 : ISBN 5-8459-0261-4 (рус.)