Visibility graph и motion planning

Visibility graph

Путь с препятствиями через трапецоидную карту

Такой путь не самый короткий

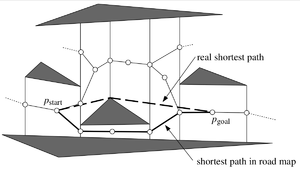
Рассмотрим задачу нахождения кратчайшего пути от точки [math] S [/math] до [math] T [/math] с препятствиями. Для начала рассмотрим движение материальной точки, случай произвольного полигона будет позднее. Для нахождения можно построить трапецоидную карту, соединить ребрами середины вертикальных сторон с центрами трапецоидов и в этом графе любым алгоритмом поиска кратчайших путей (например, алгоритмом Дейкстры или A*) найти путь от [math] S [/math] до [math] T [/math]. Но этот путь, очевидно, не будет кратчайшим.

Однако этот алгоритм обширно используется, так как трапецоидная карта дает хорошее приближение, строится за [math] O(n \log n) [/math] и занимает [math] O(n) [/math] памяти, в то время как точные решения в лучшем случае работают за [math] O(n^2) [/math] и требуют [math] O(n^2) [/math] памяти.

Лемма:

Любой кратчайший путь от [math] S [/math] до [math] T [/math] с полигональными препятствиями представляет собой ломаную, вершины которой — вершины полигонов.

Доказательство:

[math]\triangleright[/math]

Short cut Пусть кратчайший путь — не ломаная. Тогда рассмотрим участок пути, где он не является прямым. По неравенству треугольника в окрестности этого участка мы сможем немного срезать. Значит этот путь не кратчайший. Противоречие, значит лемма доказана.

[math]\triangleleft[/math]

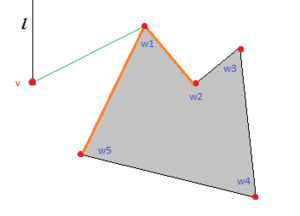
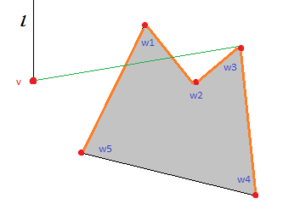
Таким образом для нахождения точного решения определим visibility graph. Его вершины — вершины полигонов. Между вершинами [math] u [/math] и [math] v [/math] существует ребро, если из [math] u [/math] видна (mutually visible) [math] v [/math] (ребра полигонов тоже входят в этот граф). К множеству вершин графа нужно добавить [math] S [/math] и [math] T [/math], а также ребра в видимые из них вершины полигонов. В получившемся графе опять же любым алгоритмом находим кратчайший путь. По лемме любое ребро кратчайшего пути — ребро visibility графа, так что мы нашли то, что нужно.

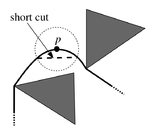
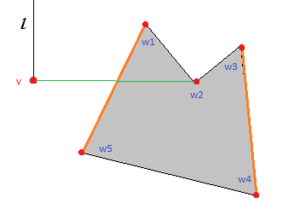
Чтобы уменьшить объем графа, из него можно удалить ребра, по которым точно не пройдет путь.

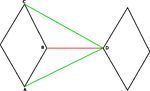
Лемма:

Если существуют вершины [math] A, B, C [/math] одного препятствия и вершина [math] D [/math] такая, что поворот [math] DBA [/math] не совпадает с поворотом [math] DBC [/math], то ребро [math] DB [/math] можно удалить. (См. поясняющую картинку справа)

Доказательство:

[math]\triangleright[/math]

Путь проходящий через ребро [math] BD [/math] будет длиннее, чем через соседей точки [math] B [/math], так как по неравенству треугольника [math] AB + BD \lt AD [/math]

[math]\triangleleft[/math]

Удаляем [math] BD [/math]

Файл:EdgeNotToDelete.jpg Не удаляем [math] BS [/math]

Построение visibility графа

Наивный алгоритм. [math] O(n ^ 3) [/math]

Если делать наивно, т. е. для каждой пары вершин проверять можно ли добавить ли такое ребро(нет ли пересечений с полигонами), будет [math] O(n^3) [/math].

Lee’s Algorithm. [math] O(n ^ 2 \log n) [/math]

Заметание плоскости вращающимся лучом

Обновление статуса заметающей прямой

Обновление статуса заметающей прямой

Обновление статуса заметающей прямой

Однако можно это сделать за [math] O(n ^ 2 \log n) [/math]. Для каждой вершины найдём все видимые из неё вершины при помощи метода плоского заметания. Нам нужно решить следующую задачу: на плоскости дано множество отрезков (рёбер препятствий) и точка [math] p [/math]. Найти все концы отрезков, видимые из точки [math] p [/math]. Будем заметать плоскость вращающимся лучом с началом в точке [math] p [/math]. Статусом заметающей прямой будет отрезки, которые её пересекают, упорядоченные по возрастанию расстояния от точки [math] p [/math] до точки пересечения. Точками событий будут концы отрезков. Итак, первым делом вершины [math] w \in W [/math] сортируются по углу между лучом [math] vw [/math] и вертикальной полуосью, проходящей через [math] v [/math]. Затем происходит инициализация множества видимых вершин (по умолчанию такое множество пустое). Далее начинается заметание плоскости. В порядке сортировки вершин для каждой из них выполняется проверка: видна ли вершина [math] w [/math] из вершины [math] v [/math]. Для этого нам достаточно проверить только пересечение с ближайшим отрезком в статусе, а он находится в корне сбалансированного дерева, т. е. эта проверка выполняется за [math] O(1) [/math]. Если вершина видима, необходимо добавить её в список видимых вершин. И, наконец, вне зависимости от видимости вершины, необходимо изменить статус заметающей прямой. Для этого, для текущей вершины [math] w [/math] необходимо удалить из списка текущих пересечений все рёбра (отрезки), которые заканчиваются в этой вершине (лежат слева от прямой [math] vw [/math]) и добавить все рёбра (отрезки), которые в ней начинаются (лежат справа от прямой [math] vw [/math]).

Вершин у нас [math] O(n) [/math], сортируем за [math] O(n \log n) [/math] плюс запросы в дереве за [math] O(n) * O(1) [/math]. Итого [math] O(n^2 \log n) [/math]. Что и требовалось доказать.

Overmars and Welzl’s Algorithm [math] O(n ^ 2) [/math]

visibility graph при помощи rotation tree

C помощью rotation tree можно достичь асимптотики [math] O(n^2) [/math].

Motion planning

Раздуваем препятствия

Ищем путь для точки

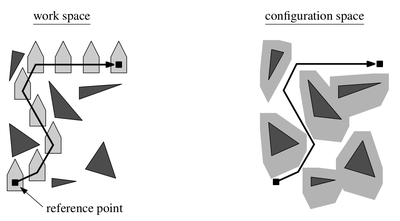
Тут мы двигаем не точку, а произвольный выпуклый полигон. Если мы его не можем вращать, просто считаем configuration space, т. е. "обводим" препятствия нашим полигоном (делаем сумму Минковского препятствий и полигона, сдвинутого в начало координат какой-нибудь точкой) и получаем другие препятствия, но зато теперь мы двигаем точку. А это мы уже научились делать выше.

Теперь рассмотрим случай, когда мы можем вращать полигон. Для начала построим трапецоидную карту, как будто мы не можем вращать полигон. Теперь будем вращать полигон на малый угол, пока он не сделает полный оборот вокруг своей оси, и для каждого угла сделаем трапецоидную карту. Теперь разместим(мысленно) все карты друг над другом. Таким образом получится, что поворот на малый угол — это движение вверх/вниз между слоями. Осталось попересекать соседние слои и добавить между ними ребра (помним что первый и последний слои одинаковы) и уже в этом графе найти путь.

При такой реализации в некоторых случаях у нас может возникнуть ошибка в повороте, так как в одной плоскости мы все можем делать точно: положения на соседних слоях могут допускаться, а повернуть мы не сможем. Это лечится в основном двумя способами: измельчением угла поворота и изначальным сглаживанием углов полигона — повращать полигон на [math] +\epsilon [/math] и [math] -\epsilon [/math] и объединить с исходным, получив новый полигон.

Так как эта задача достаточно ресурсоемка, мы рассматриваем только наличие пути, а не нахождение кратчайшего.

Источники

• Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 15 page 324-331
• статья про visibility graphs
• Хабр