Кратчайший путь в ациклическом графе

Материал из Викиконспекты
Перейти к: навигация, поиск

Пусть дан ациклический ориентированный взвешенный граф. Требуется найти вес кратчайшего пути из u в v

Определение:
Кратчайший путь из u в v – это такой путь из u в v, что его суммарный вес входящих в него ребер минимален

Решение

Пусть [math]d[/math] — функция, где [math]d(i)[/math] — вес кратчайшего пути из [math]u[/math] в [math]i[/math]. Ясно, что [math]d(u)[/math] равен [math]0[/math]. Пусть [math]w(i, j)[/math] - вес ребра из [math]i[/math] в [math]j[/math]. Будем обходить граф в порядке топологической сортировки. Получаем следующие соотношения:

[math] d(i) = \min\limits_{\mathop{j:j \rightsquigarrow i}} (d(j) + w(j, i)) [/math]

Так как мы обходим граф в порядке топологической сортировки, то на [math]i[/math]-ом шаге всем [math]d(j)[/math] ([math]j[/math] такие, что существует ребро из [math]j[/math] в [math]i[/math]) уже присвоены оптимальные ответы, и, следовательно, [math]d(i)[/math] также будет присвоен оптимальный ответ.

Реализация

Реализуем данный алгоритм: 

 //w — матрица смежности
 //d — массив кратчайших расстояний 
 //p — массив индексов вершин графа в порядке топологической сортировки
 for i = 1 .. n
   d[i] = infinity
 d[u] = 0 // где u — начальная вершина

 p = topSort(w) //топологическая сортировка графа
 for i = 1 .. n
   for j: есть ребро из p[i] в j
     d[j] = min(d[j], d[p[i]] + w[p[i]][j])

Пример

Граф из примера

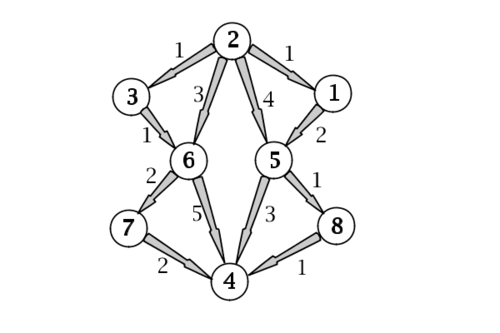
Пусть дана матрица смежности графа w со следующими весами ребер:

1 2 3 4 5 6 7 8
1 - - - 5 - - - -
2 1 - 1 - 4 3 - -
3 - - - - - 1 - -
4 - - - - - - - -
5 - - - 3 - - - 1
6 - - - 5 - - 2 -
7 - - - 2 - - - -
8 - - - 1 - - - -

Требуется найти путь из 2 в 4.
Массив p будет выглядеть следующим образом:

1 2 3 4 5 6 7 8
2 3 6 7 1 5 8 4

Массив d будет выглядеть следующим образом:

1 2 3 4 5 6 7 8
1 0 1 5 3 2 4 4

Ответ равен 5.

Альтернативный способ решения

Задачу так же можно решить поиском в ширину. Для этого будем поддерживать массив кратчайший расстояний от начальной до текущей вершины. Обходя граф, будем для каждой вершины обновлять ответы у ее сыновей как минимум из старого значения и пути, проходящего через текущую вершину.

В силу особенности обхода графа, когда происходит обновление сыновей вершины, для нее самой уже найден оптимальный ответ.

Смотри также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Кратчайший_путь_в_ациклическом_графе&oldid=42177»