Укладка графа на плоскости

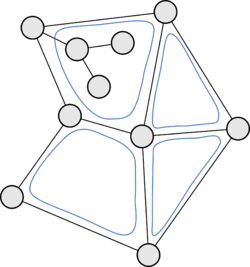Пример планарного графа. Синим контуром обозначены грани, за исключением внешней грани (всего 5 граней). Обратите внимание, что внутри грани могут содержаться другие ребра и вершины.

Определение: Граф обладает укладкой в пространстве $L$, если он изоморфен графу, вершинами которого являются некоторые точки пространства, а ребрами — жордановы кривые , соединяющие соответствующие вершины, причем Кривая, являющаяся ребром не проходит через другие вершины графа, кроме вершин, которые она соединяет; Две кривые, являющиеся ребрами, пересекаются лишь в вершинах, инцидентных одновременно обоим этим ребрам. Соответствующий граф, составленный из точек пространства и жордановых кривых из $L$, называют укладкой исходного графа. Определение: Граф называется планарным (англ. planar graph), если он обладает укладкой на плоскости. Плоским (англ. plane graph, planar embedding of the graph) называется граф уже уложенный на плоскости.

Определение: Плоский граф разбивает плоскость на несколько областей, называемых гранями (англ. faces). Одна из граней не ограничена, ее называют внешней гранью, а остальные — внутренними гранями. Для плоских графов есть простое соотношение, называемое формулой Эйлера: $V - E + F = 2$, где $V$ — вершины (vertex), $E$ — ребра (edges), $F$ — грани (faces). Это свойство позволяет в некоторых случаях просто доказывать непланарность некоторых графов, например непланарность $K_5$ и $K_{3,3}$. Понятно, что любой граф, содержащий подграф $K_5$ или $K_{3,3}$ непланарен. Оказывается, верно и обратное утверждение, но для его формулировки потребуется вспомогательное определение:

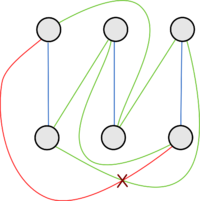Полный двудольный граф $K_{3,3}$. Этот граф непланарен, и его не получится изобразить на плоскости без пересечений ребер.

Определение:

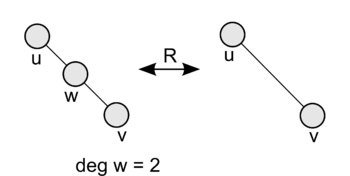
Введем отношение $R$ следующим образом: два графа на находятся в отношении $R$, если один можно свести к другому заменой вершины степени 2 на ребро между вершинами смежными ей, или наоборот, добавлением вершины степени два на ребро (см. картинку). Отношением гомеоморфизма (или топологической эквивалентности) назовем транзитивное замыкание отношения $R$: $R$*.

Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных $K_5$ и $K_{3,3}$: теорема Понтрягина-Куратовского.

Теорема:

В трехмерном евклидовом пространстве любой граф укладывается.

Доказательство:

$\triangleright$

Все вершины произвольного графа $G$ помещаем в различных точках координатной оси $OX$. Рассмотрим пучок плоскостей, проходящих через ось $OX$, и зафиксируем $|E|$ различных таких плоскостей. Теперь каждое ребро $(u, v)$ изобразим полуокружностью, проходящей в соответствующей плоскости через вершины $u, v$. Ясно, что различные ребра не будут пересекаться кроме как в общих вершинах.

$\triangleleft$

См. также

• Формула Эйлера

Источники информации

• Асанов М, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы
• Харари, Ф. Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009. — С. 126. — ISBN 978­-5­-397­-00622­-4.