Байесовские сети
Версия от 21:51, 9 марта 2019; Evgeniya Katunina (обсуждение | вклад)
| Определение: |
| Байесовская сеть (англ. Bayesian network) — это направленный ациклический граф , в котором каждой вершине поставлена в соответствие случайная переменная и каждое ребро представляет прямую зависимость от . Пусть , тогда в Байесовской сети каждой вершине графа должно быть сопоставлено распределение условных вероятностей от вершин из . |
Цепное правило для Байесовских сетей:
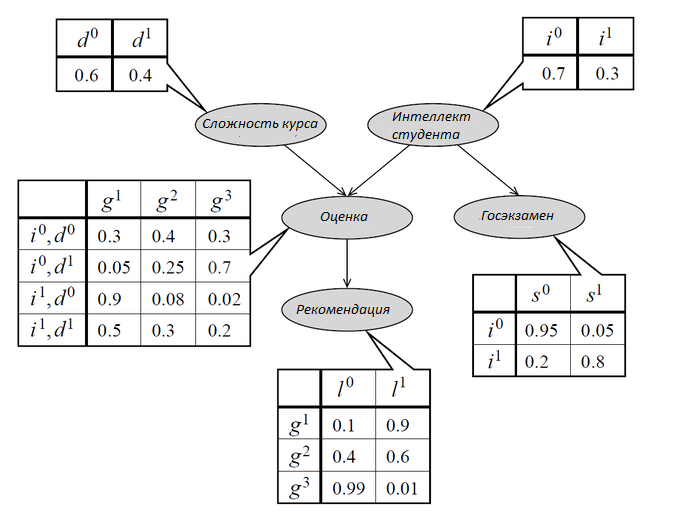
Пример
Оценка студента (Grade) зависит от его интеллекта (Intelligence) и сложности курса (Difficulty). Студент просит у преподавателя рекомендательное письмо (Letter), предположим, что преподаватель может написать плохое или хорошее письмо в зависимости от оценки студента. Также студент сдаёт экзамен для поступления в колледж (SAT), результаты экзамена не зависят от письма преподавателя, оценки за его курс и сложности курса. Представление этой модели в Байесовской сети представлено на рисунке ниже.
С помощью цепного правила рассчитаем вероятность того, что умный студент получает B по лёгкому курсу, высокий балл по SAT и плохое рекомендательное письмо: