Существенно неоднозначные языки

Неоднозначные грамматики

Неоднозначной грамматикой называется грамматика, по которой для одной цепочки существует более одного дерева разбора.

Пример:

Рассмотрим грамматику [math]E \rightarrow E + E | E * E[/math] и выводимую цепочку[math]E + E * E[/math]. Ее можно вывести двумя способами:

[math]E \Rightarrow E + E \Rightarrow E + E * E[/math]

[math]E \Rightarrow E * E \Rightarrow E + E * E[/math]

Эта граматика неоднозначна.

Существенно неоднозначные языки

Язык называется существенно неоднозначным, если любая его грамматика неоднозначна. Пример такого языка: [math]0^a 1^b 2^c[/math], где [math]a=b \vee b=c[/math] Докажем, что [math]\forall \Gamma \exists k: 0^k 1^k 2^k[/math] имеет хотя бы 2 дерева разбора.

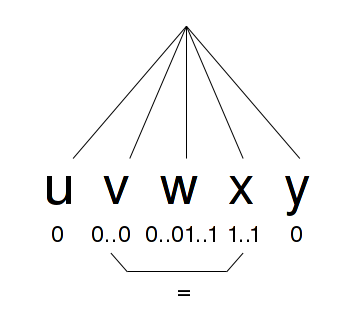
Лемма: [math]\forall \Gamma : \exists k \ge 1: z \in L(\Gamma), |z| \ge k[/math] и в z выбраны хотябы k позиций, то z представимо в виде [math]z = uvwxy[/math], где [math]uvw[/math] или [math]wxy[/math] содержат хотя бы по одной выбранной позиции и [math]vwx[/math] содержит не более k выбраных позиций и [math]\exists A[/math] - нетерминал, такой, что [math]\forall i: S \Rightarrow^* uAy \Rightarrow^* uvAxy \Rightarrow^* uv^i Ax^i y \Rightarrow^* uv^i wx^i y[/math].

Доказательство:

Пусть в грамматике m нетерминалов, длина всех правых частей не превосходит l, значит высота дерева разбора хотя бы 2m+1.

Выбираем [math]k=l^{2m+3}[/math]

Вершина ветвится, если хотя бы 2 ребенка.

Если есть сын с помечеными детьми в поддереве - идем в него, ветвится - идем где больше.

Вершина ветвится влево, если слева от него есть помеченные листья. Так же определяеся ветвление вправо.

Одного из этих типов хотя бы m+2.

Пусть m+2 ветвится влево. Рассмотрим нижние m+1 - среди них встретится повторяющийся нетерминал A. Для него уже выполнено условие леммы. В частности uvw - помечены. Из всех прочих выбираем один, в средней части не более k помеченных.

Лемма доказана.

Неоднозначность:

Возьмем k, слово [math]0^k 1^k 2^{k+k!}[/math], пометим первые k нулей.

По лемме можно разбить на 5 частей.

По лемме можно породить слово [math]0^{k+k!} 1^{k+k!} 2^{k+k!}[/math].

[math]i = \frac{n!}{t} + 1[/math]

Аналогичные рассуждения справедливы для слова [math]0^{k+k!} 1^k 2^k[/math], в котором отмечены все двойки. Пусть в нем повторяющийся нетерминал B. Очевидно, что А и В - разные деревья и одно не является потомком другого. Тогда если дерево разбора в обоих случаях одиниково, то оно порождает слово вида [math]0^{k+k!+t} 1^{k+k!+t+r} 2^{k+k!+r}[/math], что не так.

В результате мы имеем 2 дерева разбора для одного слова. Значит язык существенно не однозначен.

Теорема:

Для языка принимаемого ДМП-автоматом существует однозначная КС-грамматика